Linear Regresssion
Sung Kim 교수님 강의로 공부하는 머신러닝 Section 2,3
Linear regression
x와 y가 linear relationship을 가진다고 판단이 들 때, 일차방정식 형태의 가설을 세워 모델링하는 것이다.
Hypothesis
$H(x)=Wx+b$ 가설은 일차방정식의 형태를 띈다. W는 weight, slope(기울기)이고 b는 bias, intercept(절편)이다.
Simplified hypothesis: 이를 간소화해서 $H(x)=Wx$로 나타내기도 한다.
Residual(잔차)
잔차는 $H(X)-y$, 모델에서 예측한 값 - 실제 예측한 값이다.
RSS(residual sum of squares)
잔차는 음수가 될 수도, 양수가 될 수도 있기 때문에 square처리해서 모든 잔차를 더한다. RSS를 식으로 나타내면 $\sum_{i=1}^m (H(X_i)-y_i)^2$이다.
Cost function
$cost(W,b) = 1/m * \sum_{i=1}^m (H(X_i)-y_i)^2$
좋은 모델을 위해서는 잔차를 최소화 해야한다. 이 잔차 합의 평균을 구하는 함수를 Cost function이라고 부르는데, 이 cost를 minimize 하는 w,b를 찾아야한다. 이 식은 결국 모델의 Total Error를 보여준다고 할 수 있겠다. 이 식은 Mean Squared Error라고도 불린다.
Simplified cost function: bias를 고려하지 않고 $cost = 1/m * \sum_{i=n}^m (W(X^i)-y^i)^2$로 나타내기도 한다. Cost function은 Loss function이라고도 불린다.
Gradient descent algorithm(경사 하강법)
Cost function을 minimize하는 w,b를 찾아내는 알고리즘
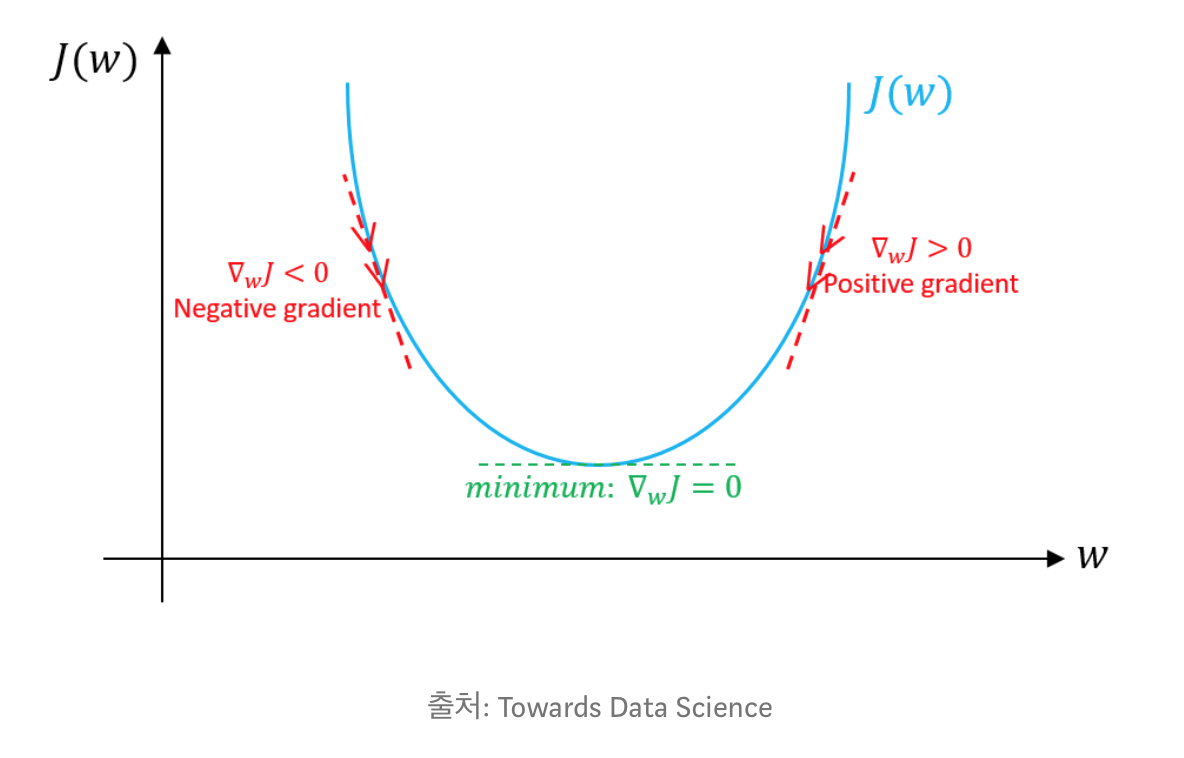
Gradient는 경사를, Descent는 내려간을 의미한다. 경사도를 따라서 내려가다가 경사도가 0이 되었을 때 stop하는 알고리즘이라고 할 수 있다.
- 0,0에서 시작 (또는 다른 값에서 시작)
- W,b 을 조금 바꾸고 줄일 수 있는지 확인한다.
- 파라미터 (W,b)를 바꿀때마다 cost(W,b)를 가장 줄일수 있는 경사도 (gradient)를 선택한다.
- 미분을 이용해 구하는데, tensorflow에서 자체적으로 구해주기 때문에 걱정 안해도 된다.
W := W - a(cost(W)를 미분한 값)
- descent가 +이면, -로 이동, descent가 -이면, +로 이동
- 기울기가 음수이면 W의 변화량이 양수가 되므로 오른쪽으로 이동, 기울기가 양수이면 W의 변화량이 음수가 되므로 왼쪽으로 이동
여기서 a(alpha)는 learning rate라고 불리는, step을 조절하는 값이다.
Learning rate를 적절하게 설정해야 하는 이유는 다음과 같다.
- Learning rate가 너무 크면, 발산해버리는 경우가 발생한다. (Overshooting)
- Learning rate가 너무 작으면, 일단 수렴하는 속도가 너무 느리고, local minimum에 빠질 확률이 증가한다.
이것이 training의 원리이다.
- random weights로 training을 시작하고.
- 기울기의 반대 방향으로 weights를 수정하며 training 시킨다.
Delta Rule
The delta rule learning formula for weight adjustment.
\[∆𝑤 = c(t_i-f(net_j))f'(net_j)x_k\]- $c$ = learning rate
- $t_i$ = desired output
- $f(x)$ = actual output values of the $i_\text{th}$ node
- $f’$ = The derivative
- $x_k$ = the $k_\text{th}$ input to node i
Convex function
시작점에 상관없이 도착점이 같은 function
Cost function은 convex function이여야 한다. 확인하고 GDA를 사용해야한다! 하지만 다행히 우리 hypothesis가 convex function이기 때문에 늘 minimum을 찾을 수 있다.