Sung Kim 교수님 강의로 공부하는 머신러닝 Section 4

Multi-variable linear regression

x1, x2, x3와 같이 여러개의 input이 있는 multi-variable regression

결국, 변수가 여러 개일 때 사용하는 선형 회귀이다. 주로 여러 개의 x값으로 하나의 y값을 예측하는 경우가 많다.


Hypothesis

$H(x1,x2,x3)=w1x1+w2x2+w3x3+b$

다변수 선형회귀에서는 변수들을 매트릭스로 묶어서 연산한다. 이 때, 연산에는 Matrix multiplication이 쓰인다. 위의 Hypothesis 를 Matrix multiplication으로 표현하면 다음과 같다.

\[[X]\times[W] = [H(X)]\]

\[H(X)=XW\]

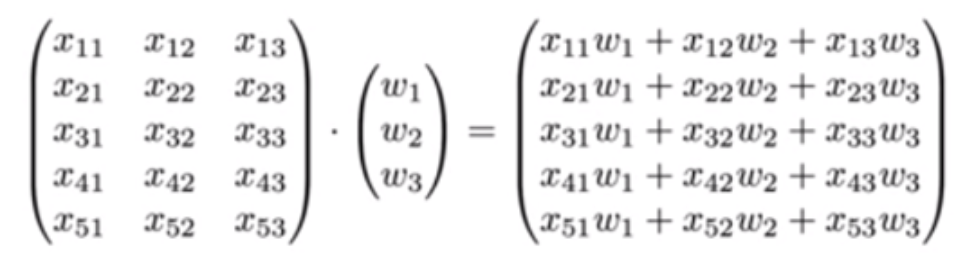
위 식은 $[5, 3] \times [3, 1] = [5, 1]$의 shape를 갖는다. 이를 일반화하면, [instance 개수, X 개수] X [X 개수, Y개수] = [instance 개수, Y 개수]이다.

주로 instance는 가변적인 값을 가지기 때문에 n이나 -1 (NumPy), None (TensorFlow)로 표현한다.

W 매트릭스의 행이 X의 변수 개수, 열이 Y의 변수 개수인 점도 기억해두면 좋다. 그리고 이론적으로는 $H(x)=W \times +b$로 쓰지만,


WX v.s. XW

Theory

\[H(x)=WX+b\]

Implementation (Tensorflow)

\[H(X)=XW+b\]

둘은 같지만, 실제로 텐서플로에서는 두번째 식을 사용한다. 별도의 처리 없이 행렬곱셈 계산이 가능해서 더 편하기 때문이다.