Neural Network: XOR Problem, Back Propagation

Sung Kim 교수님 강의로 공부하는 머신러닝 Section 9

Neural Nets (NN) for XOR

하나의 logistic regression unit은 XOR을 split하지 못해, 해당 문제를 해결할 수 없었다. 하지만 여러 개면 해결 가능했다. 하지만, 문제는 각각의 복잡한 네트워크의 w, b의 학습이 불가능하다는 것이었다.

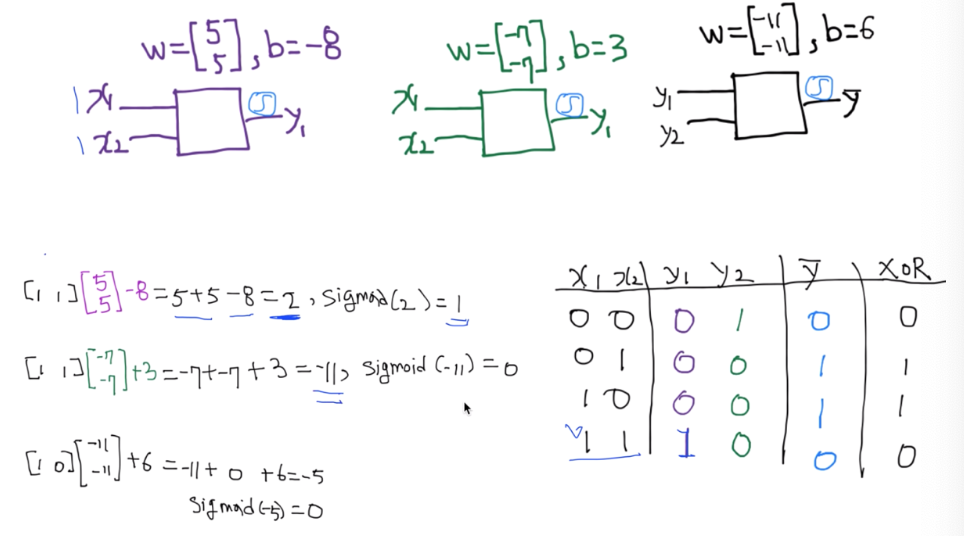
nn_for_xor

위처럼 3개의 유닛으로 XOR 문제를 풀 수 있다. 이 전체를 하나의 neural network라고 부르고, 네모 박스를 unit/gate/perceptron이라고 부른다.

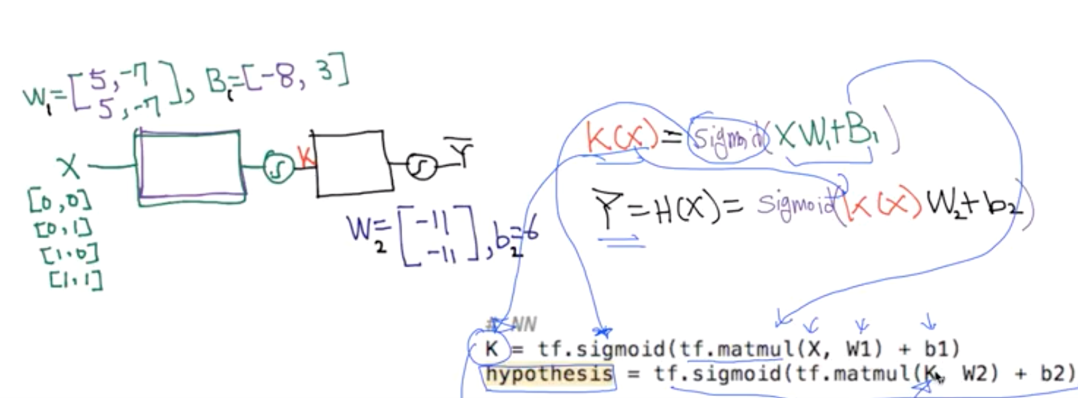
nn_for_xor_2

Neural network와 그 hypothesis를 위와 같이 정리할 수 있다. 여기서는 모든 weight과 bias가 주어졌지만, 실제로 모델은 어떻게 이 weight과 bias를 학습할까?

Partial derivative

우리말로는 편미분, 이 미분 기법은 backpropagation 알고리즘에서 매우 중요하다.

Consider other variables as constants
일변수 함수가 아니라 다변수 함수에서 하나의 변수만을 기준으로 하고 나머지 변수는 상수 로 보는 미분을 편미분이라고 한다.

예시를 보자.

$f(x)=2x$ 이를 미분한 값은 2이다.

$f(x,y)=xy,\frac{\partial f}{\partial x}$ 이 식에서는 x를 편미분해야하기 때문에 y를 상수 취급 해준다. 따라서 값은 y이다.

$f(x,y)=xy,\frac{\partial f}{\partial y}$ 이 식에서는 y를 편미분해야하기 때문에 x를 상수 취급 해준다. 따라서 값은 x이다.

더 공부하기 전에 몇 가지 미분을 복습해보자.

$f(x)=x+x$를 미분하면 $1+1=2$, $f(x)=x+3$을 미분하면 $1+0=1$이 된다.

$f(x,y)=x+y,\frac{\partial f}{\partial y}$ x를 편미분하는 것이기 때문에 y를 상수취급하므로, 값은 $1+0=1$이 된다.y가 상수이기 때문에, 상수를 미분하면 0이 됨에 주의하자.

Chain Rule

\[f(g(x))=\frac{\partial f}{\partial x} = \frac{\partial f}{\partial g} \bullet \frac{\partial g}{\partial x}\]

뒤에 나올 backpropagation에서 이 rule을 사용한다.

Back Propagation

모든 유닛의 weight과 bias를 계산하기엔 계산량이 너무 많아서, 편미분을 통해 deep network를 학습시킨다.

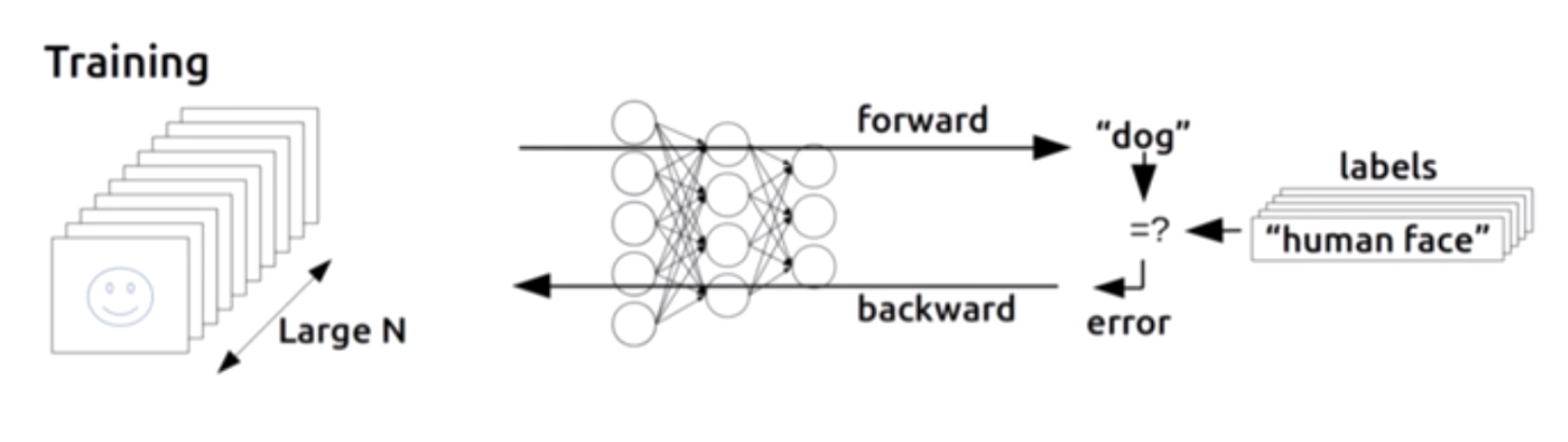
모델을 돌린다. 그리고 예측값과 실제값을 비교해서 거기서 나온 error, 즉 cost 형태로 나온 것을 뒤에서 부터 앞으로 쭉 돌린다. 그래서 미분 값과, 실제로 어떻게 무엇을 조정해내는지 알아내는 알고리즘이 backpropagation이다.

예를 들어보자.

\[f = wx + b, g=wx, f=g+b\]

위 수식을 neural network로 표현하면 다음과 같다.

bp2

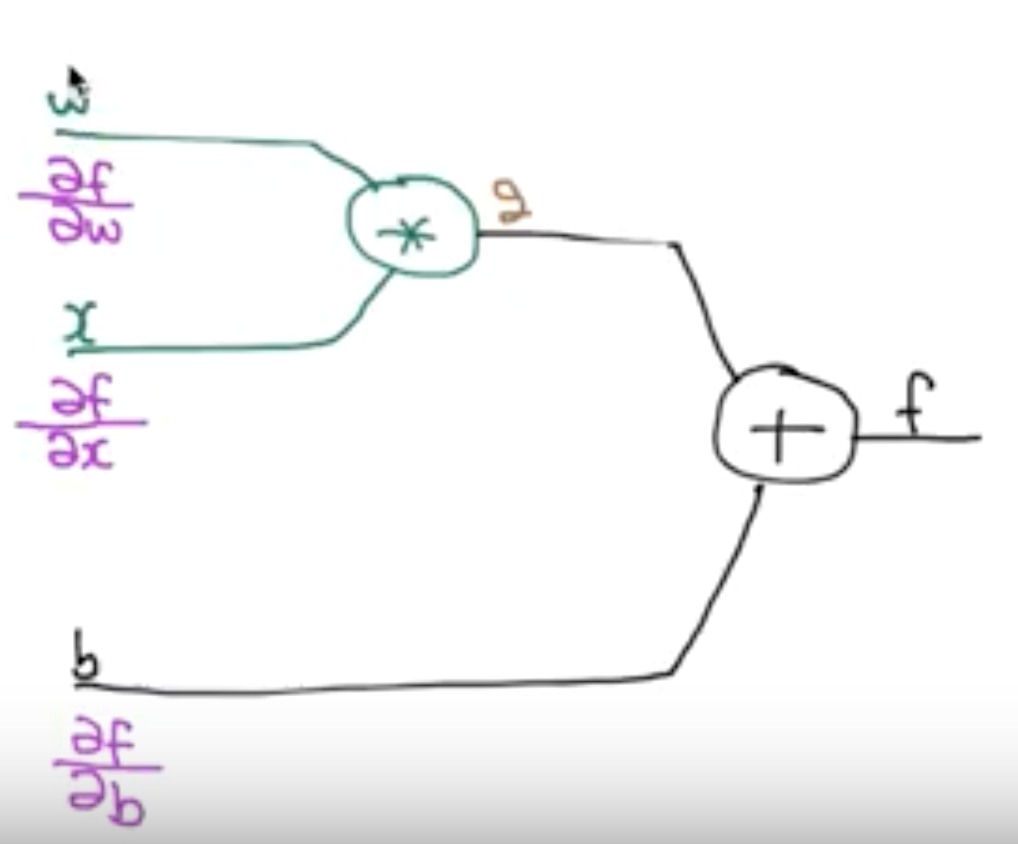
$w, x, b$ 각각이 $f$에 미치는 영향을 구하고 싶을 때, 그것이 각각 $\frac{\partial f}{\partial w}, \frac{\partial f}{\partial x}, \frac{\partial f}{\partial b}$가 될 것이다.

bp3

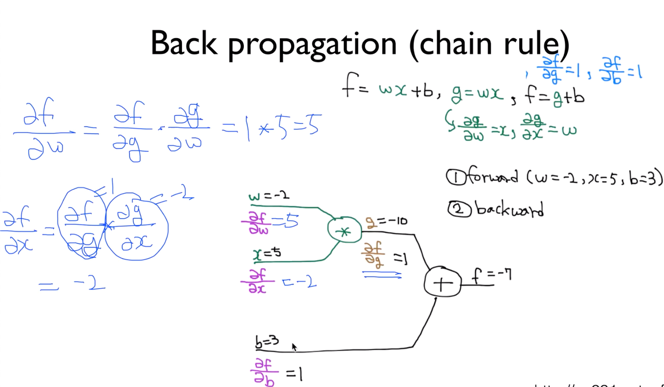
다음과 같은 순서로 진행한다.

g와 f의 값을 주어진 w,x,b의 값을 통해 구한다.
g가 f에 미치는 영향, $\frac{\partial f}{\partial g}$를 구하고, b가 f에 미치는 영향, $\frac{\partial f}{\partial b}$을 구한다.
chain rule을 이용해 $\frac{\partial f}{\partial w}, \frac{\partial f}{\partial x}$의 값도 구한다.

$\frac{\partial f}{\partial w}$의 값이 5가 나왔는데, 이는 $w$값이 1만큼 바뀌면 $f$의 값이 5만큼 바뀐다는 것이다. 이 미분한 값들을 보고 우리는 $w,f,b$ 사이의 관계를 조절할 수 있다.

bp4

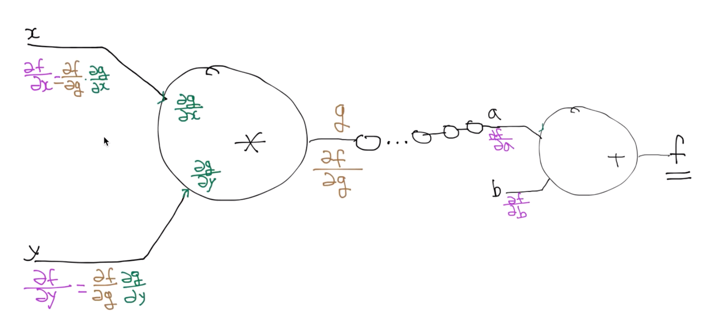
아무리 layer가 많아도 backpropagation을 이용하면 된다. 가장 먼저, 마지막 node를 계산한다. 그 다음 단계로 가서 쭉 chain rule을 적용해 backpropagation을 진행한다. 이런 식으로 진행하면, 결국 최종 입력값과 최종 출력값 사이의 관계(미분값)을 알 수 있다.

Sigmoid 미분

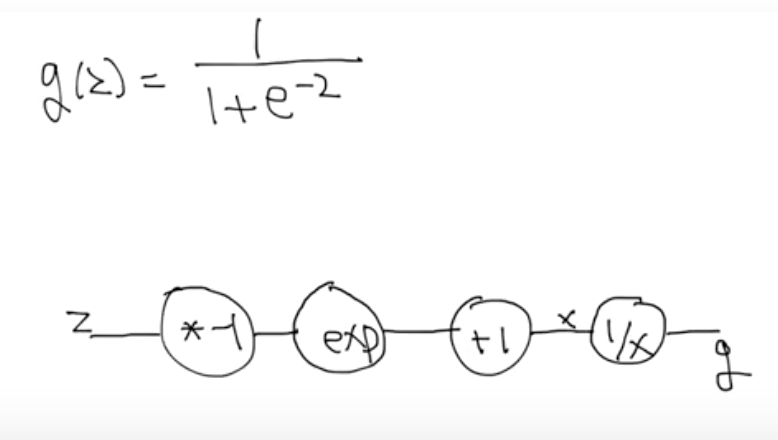
sigmoid 미분도 복잡해 보이지만, backpropagation을 이용해 해결할 수 있다. 각 파트의 미분값이 뭔지 알기 때문에, local 미분 값들을 곱해 차근차근 끝까지 미분값을 구할 수 있다.