Neural Network 2: ReLU and 초기값 정하기
Sung Kim 교수님 강의로 공부하는 머신러닝 Section 10
Let’s go deep and wide!
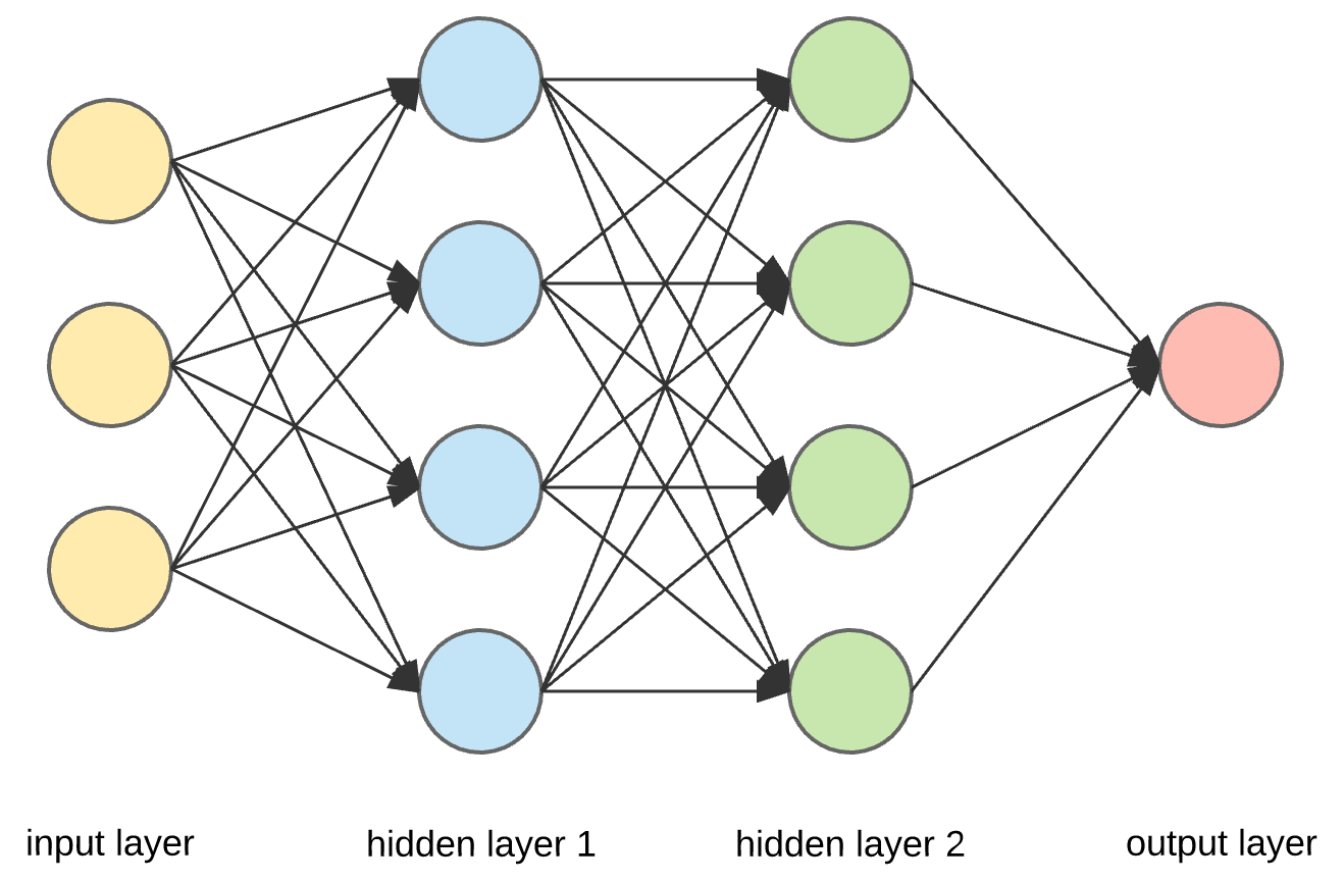
신경망은 기본적으로 다음과 같이, input layer - hidden layers - output layer의 구조로 이루어져 있다.
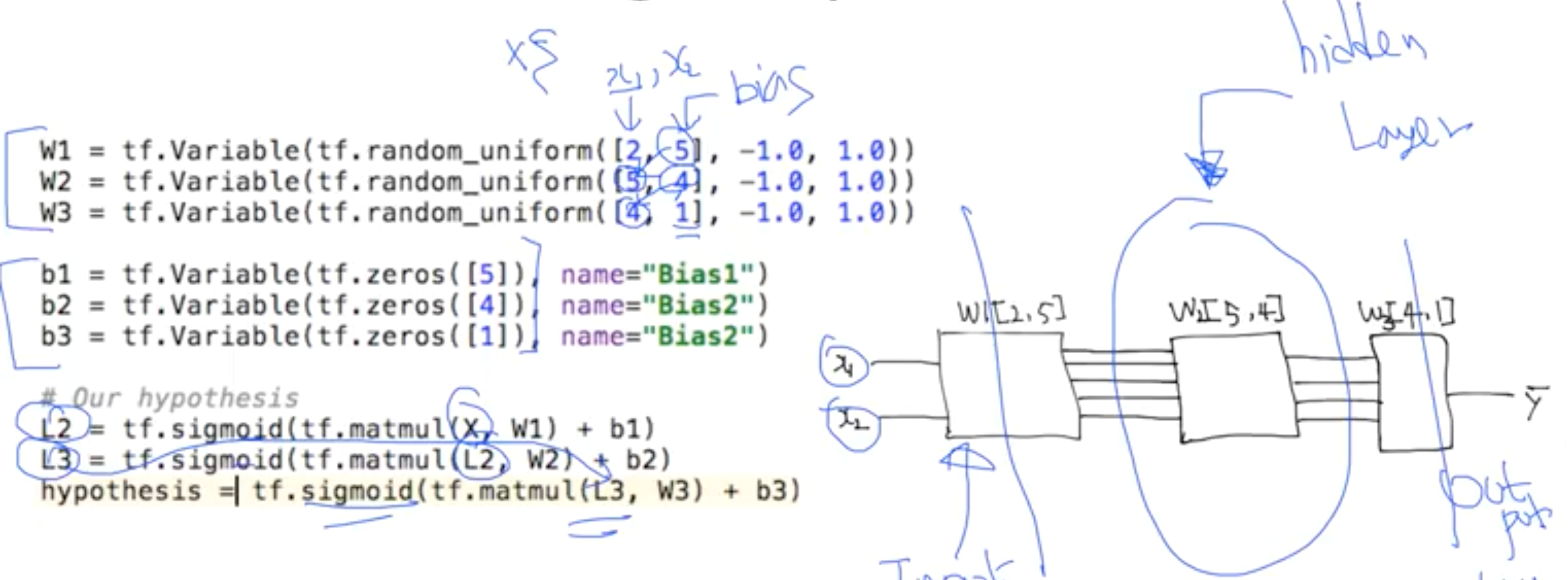
코드의 첫 줄을 살펴보면, [2, 5]에서 2sms x가 2개이기 때문에 2이고, 5는 임의로 지정해준 출력 개수이다. 아무 숫자나 상관 없다. 하지만, 그 다음 레이어에서의 입력값을 전 레이어의 출력값과 같게 맞춰줘야 한다. 그리고 마지막 레이어의 출력값은 1이 되도록 했다.
신경망은 각 Layer에서 W와 b를 사용하여 예측값(hypothesis)를 연산하고, 그 다음 Layer로 넘겨 또 다른 W와 b로 연산하여 예측값을 정교화해가는 과정을 통해 학습한다.
deep하다는 것은 레이어의 개수, hidden layer가 많다는 것이고, wide하다는 것은 한 레이어에서 뉴런의 개수를 증가시키는 것을 의미한다.
Vanishing Gradient
hidden layer의 개수가 많으면 학습이 더 많이 이루어지므로 성능이 좋아질 것 같지만, 항상 그렇지는 않다. 레이어의 개수가 증가한다고 Backpropagation의 cost, accuracy 개선량이 함께 증가하지 않는다. 2단, 3단은 성능이 좋지만 너무 deep하면 오히려 성능이 떨어진다.
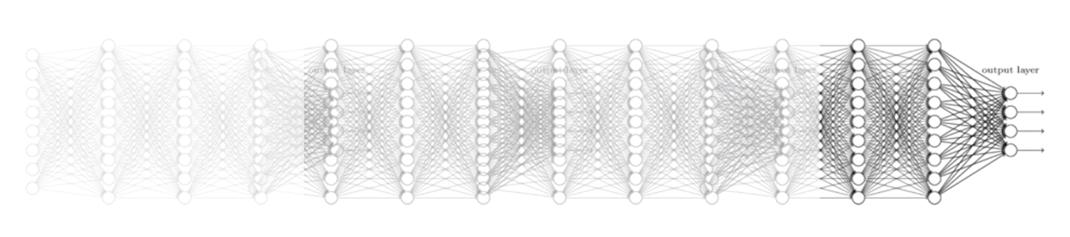
Why? Sigmoid를 계속 통과해야 하기 때문에 계산한 값이 0~1 사이에서만 계속 나오게 된다. Back propagation 과정에서 chain rule을 사용해서 미분값을 곱하는데, 0과 1사이의 작은 값을 여러번 반복해서 곱하다보면 최종 기울기가 굉장히 작은 값이 된다. 결국 최종 미분값은 0에 가까운 값이 된다. 미분값이 최종 미분값에 크게 영향을 끼치지 않는 것이다.
이를 두고 레이어 끝으로 갈 수록 기울기가 사라진다고 해서 Vanishing Gradient라고 부른다.
Geoffrey Hinton’s Summary of Findings up to today
- Our labeled datasets were thousands of times too small.
- Our computers were millions of times too slow.
- We used the wrong type of non-linearity. - (1)
- We initialized the weights in a stupid way. - (2)
- Hinton 박사는 기존에 내부 hidden layer의 activation 함수로 사용하던 sigmoid 함수에 문제가 있다고 지적했다.
- 그리고, 초기값 설정에도 문제가 있다고 지적했다.
이 두 문제점의 해결 방안을 차례로 살펴 보겠다.
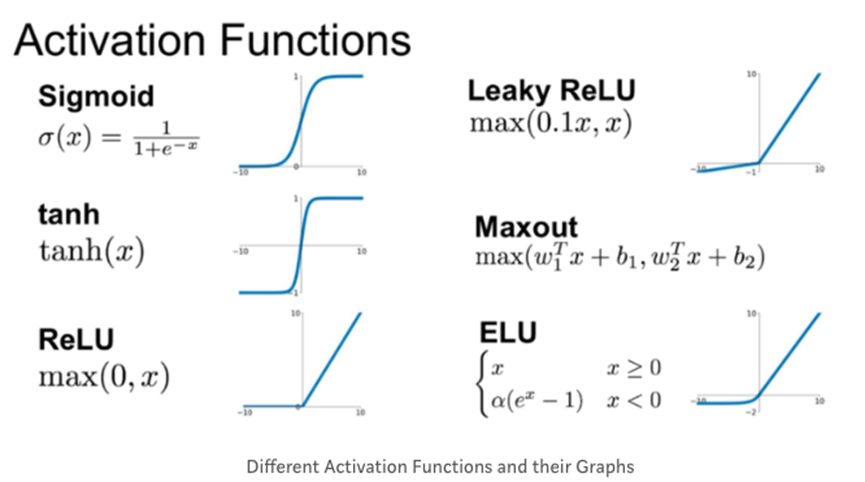
Sigmoid 대신 ReLU!
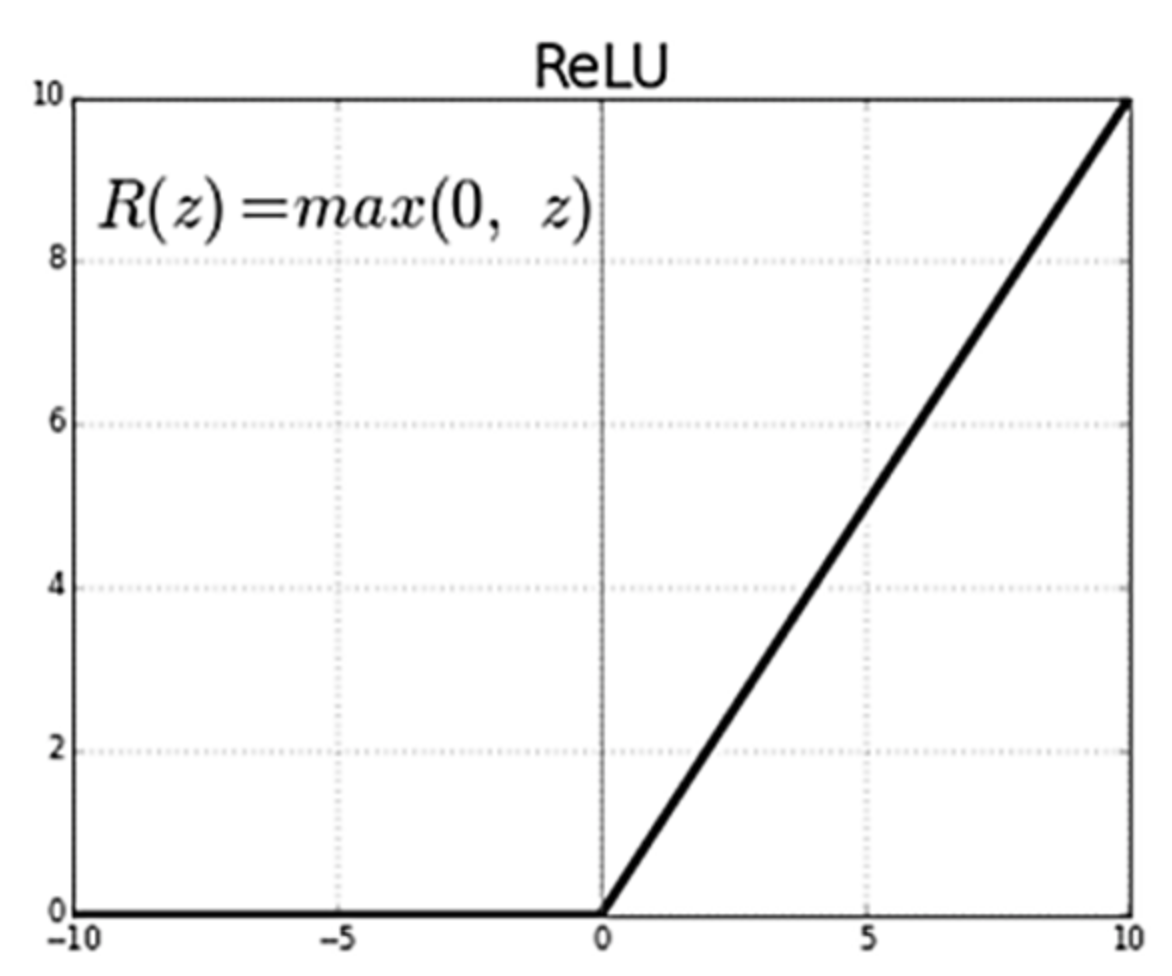
ReLU (Rectified Linear Unit) 함수는 쉽게 말해 0보다 작은 값이 나온 경우 0을 반환하고, 0보다 큰 값이 나온 경우 그 값을 그대로 반환하는 함수다.
Sigmoid는 0보다 큰 값일 경우, 1을 반환한다. 반면, 이 ReLu는 0보다 크다면, 끝까지 간다.
내부 hidden layer에는 이 ReLU를 적용하고, 마지막 output layer에서만 Sigmoid 함수를 적용한다. (최종 값은 0~1 사이의 값을 가져야 하기 때문에) 이렇게 하면 이전에 비해 정확도가 훨씬 올라간다.
물론, 이 밖에도 다양한 activation functions가 존재한다.
초기값 설정하기
아까 거론했듯이, Hinton 박사는 초기값 설정에도 문제가 있다고 지적했다.
- We initialized the weights in a stupid way
- Need to set the initial weight values wisely
- Not all 0’s
단순하게 초기값에 0을 주게 되면 Backpropagation 과정에서 0을 곱하게 되므로, 뒤의 모든 값들이 줄줄히 0이 되어 최종 기울기가 0이 되어버린다.
이에 대한 대안으로 나온 것들을 살펴보도록 하자.
1. RBM & DBN
RBM (Restricted Boatman Machine)
- 하나의 visible layer, 하나의 hidden layer, 두 레이어만 고려해 계산한다.
- 실제 input 값 $x$를 넣고 output 계산(Forward)과 output으로부터 input 값 $\hat x$ 예측(Backward)을 통해 실제 $x$값과 예측된 $\hat x$값을 비교한다.
- 반복하며 초기 W값을 최적화시킨다.
DBN (Deep Belief Network)
RBM을 중첩하여 만든 것이 DBN으로, Pre-training과 Fine-tuning 두 가지 단계로 이루어져 있다.
-
Pre-training: 여러 레이어 중 인접한 두 개 레이어끼리 순차적으로 RBM을 계산하여초기 W값을 최적화시킨다. -
Fine-tuning: 최종 label을 활용해서 학습한다. (초기값 잘 설정되었으므로 약간만 조정하면 됨)
이는 꽤 복잡하다. 다행히도, 우리는 이런 복잡한 RBM을 weight 초기화에 사용하지 않아도 된다. 이후 다른 학자들에 의해서 RBM보다 단순하지만 더 성능이 좋은 초기화 방법들이 등장한다.
2. Xavier & He initialization

간단히 말하면 입력값의 개수(fan_in)과 출력값의 개수(fan_out) 사이의 임의의 수를 Xavier는 fan_in의 루트값, He initialization 각각 fan_in, fan_in/2의 루트값으로 나누어 초기값을 구하는 방법이다.
초기화 방법에 대해서는 아직 완벽한 이론이 없고, 연구가 활발히 진행되고 있다. (Batch normalization, Layer sequential uniform variance…)
Overfitting
Overfitting 확인 방법
training set에서는 매우 낮은 error rate, test set에서는 error rate가 줄어들다가 결국 매우 높은 error rate를 보인다? Overfitting!
Overfitting 해결법!
- More training data
- Reduce the number of features
- Regularization
Regularization
Not to have too big numbers in the weight, weight가 너무 큰 값을 가지지 않도록 하는 것이다.
\[cost + \lambda\sum W^2\]위 식은 신경망 학습에서 주로 사용되는 정규화 방법인 L2 regularization이다. lambda값에 따라서 regularization의 중요도(강도)를 설정하는데, 너무 높은 값을 준다면 underfitting이 일어날 수도 있다.
Dropout
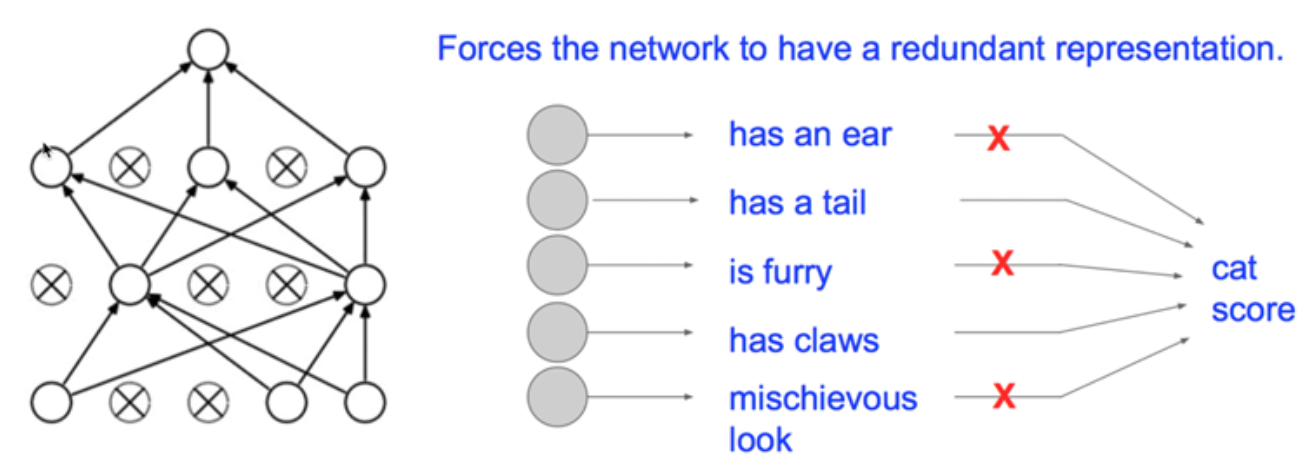
Randomly set some neurons to zero in the forward pass, 즉 랜덤하게 node를 줄여 training set의 Overfitting을 방지한다.
주의! 학습할 때만 dropout 시키는 것이므로, test set을 학습할 때는 node를 dropout하면 안 된다!

TensorFlow에서는 이렇게 구현한다. Train할 땐 dropout_rate을 0.7로, Evaluation에서는 dropout_rate를 1로 두었다는 것에 주의하자.
Ensemble (앙상블)
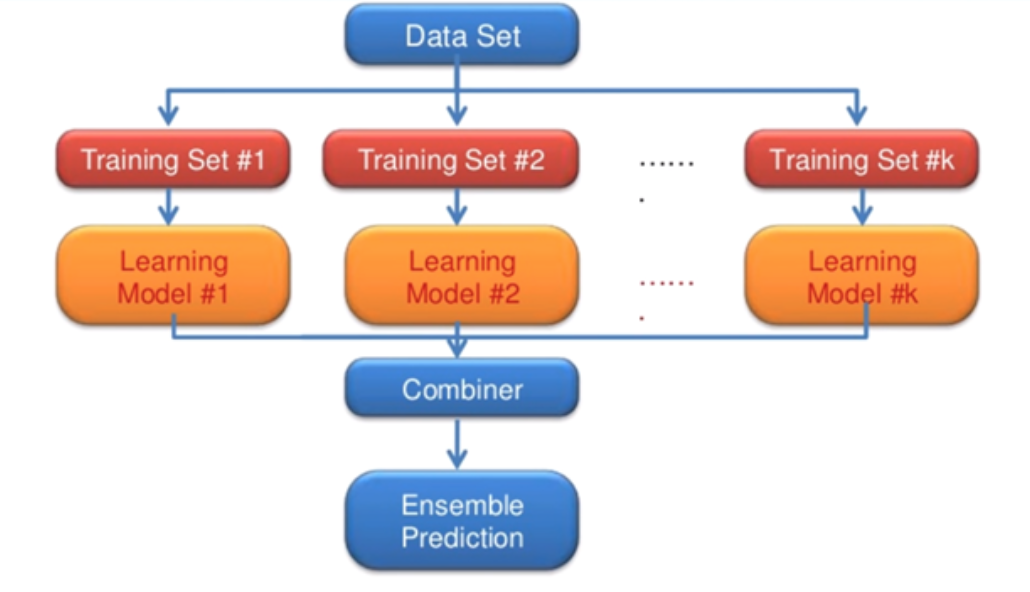
앙상블 모델은 모델을 돌릴 수 있는 리소스가 많을 때, 학습 시킬 수 있는 장비가 많을 때 사용한다.
이 예시에서는 다른 training set을 사용하지만, 같거나, 같지만 초기값은 다른 training set을 구성해 사용할 수도 있다. 이런 각각의 training set에서 각각의 learning model을 만들어, 각각 학습시킨 뒤 combine시키는 것이다. 2%에서 4~5% 정도 성능이 향상된다.
네트워크 모듈 마음껏 쌓아보기 like LEGO
Fast Forward
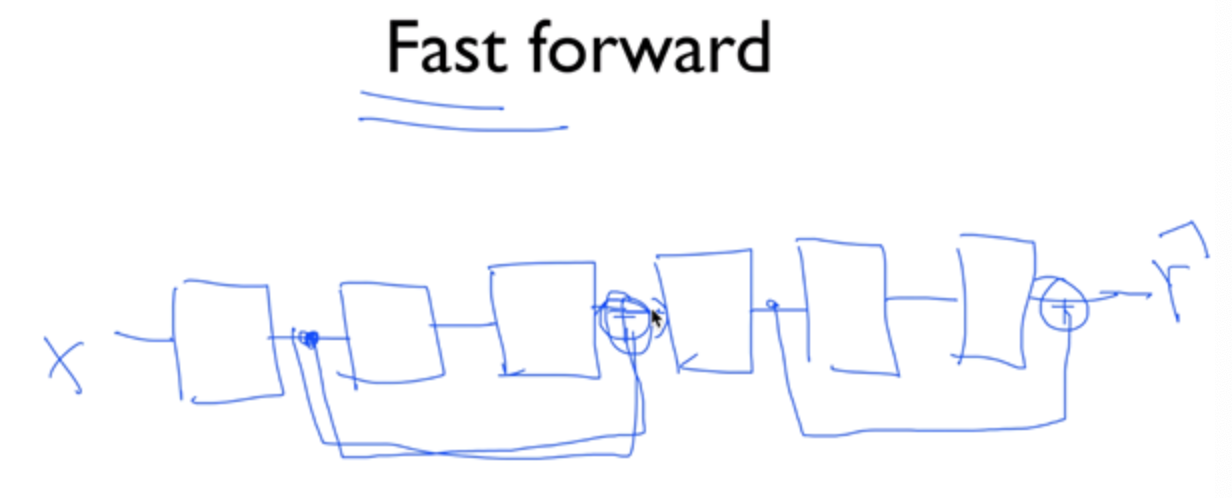
module 2개를 동시에 건너뛴다. (He)
Split & Merge
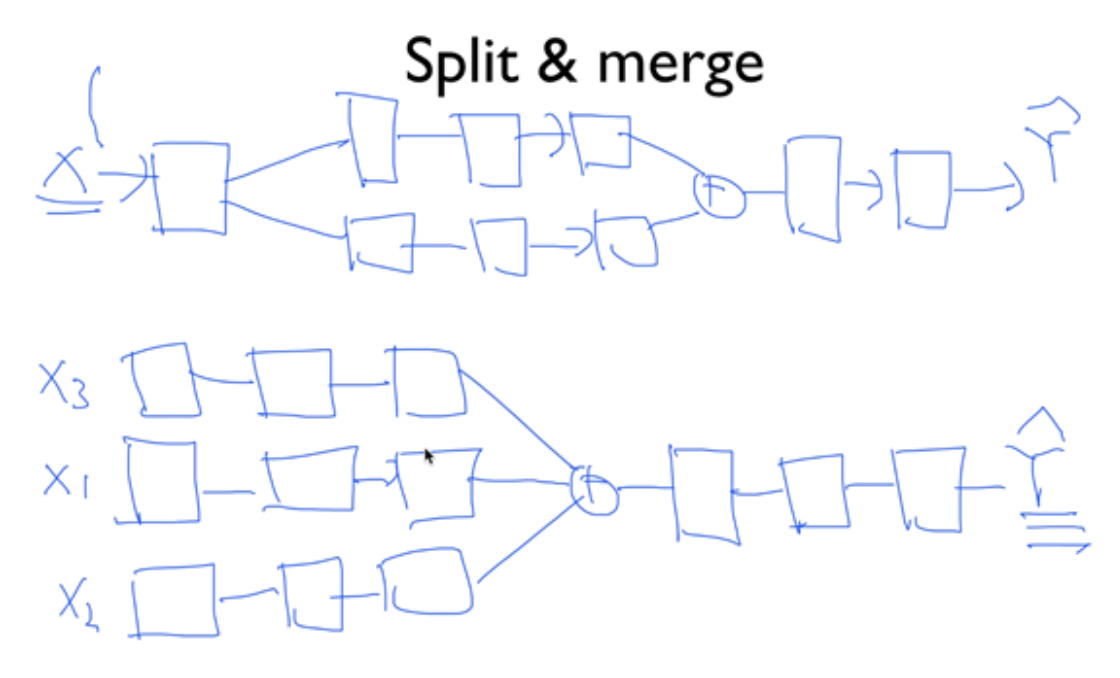
하나의 입력을 중간에 나누거나, 입력을 나누고 마지막에 합칠 수 있다. (CNN)
Recurrent Network
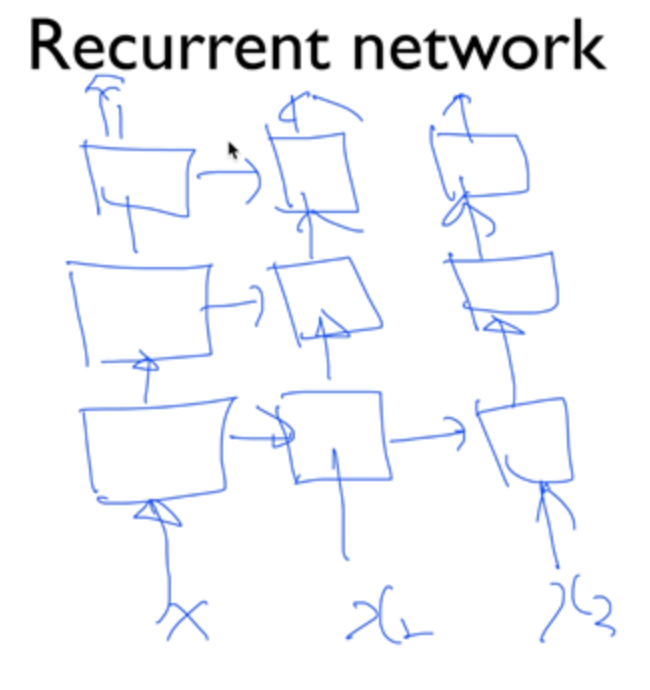
이런 구조의 네트워크도 만들 수 있다. (RNN)