Recommender systems 원서를 읽던 중에 Euclidean Distance와 Manhattan Distance가 등장했다. 두 개념을 비교하고, 왜 특정 상황에서 Euclidean Distance보다 Manhattan Distacne를 사용하는 것이 나은지 알아보자. GAN에서 사용하는 거리 개념도 살짝 맛보자.

Distance를 구하는 이유?

  • distances는 결국 일종의 similarity 개념이다. 거리가 가까우면 유사한 것, 멀면 유사하지 않은 것이다.
  • 추천 시스템은 물론, NLP 도메인에서 문서의 유사도를 구할때 등 다양한 인공지능 분야에서 널리 사용된다.
  • 데이터 특징에 맞게 적절한 metric을 선택해야 한다.


Euclidean distance

2차원이라고 가정하면 유클리드 거리를 구하는 식은 아래와 같다.

$d=\sqrt{(a_1-b_1)^2+(a_2-b_2)^2}$

기하학적으로 생각하면 L2 Norm, 점 a와 b의 최단 거리를 구하는 것이다. 대표적인 common distance metric이다.


Manhattan distance

mht

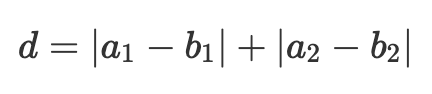
유클리드 거리와 달리, 차원의 차를 제곱하지 않고 절대값의 합으로 나타낸다. ‘Manhattan’ 이라는 이름의 유래처럼, 몇 블록 이동했는지를 계산하는 metric이라고 직관적으로 이해하자. N1 Norm이다.


유클리드 거리보다 맨하탄/맨하튼 거리가 선호되는 경우

Multidimensional and sparse data

Recommender Systems 책 peers clustering 46페이지에 잠깐 언급된 부분이다. 모든 유저가 많은 rating을 남기는 것이 아니기 때문에 유저마다 몇 개에 대해 평가를 했는지 그 수가 다를 수 있다. 이와 같은 이유로 rating matrix를 그렸을 때 유저들의 dimensions의 차이가 크다면, 유클리드보다 맨하탄을 사용하는 게 낫다라고 한다. 또는 normalized value를 사용하는 것이 better.

The use of Manhattan distance depends a lot on the kind of co-ordinate system that your dataset is using. While Euclidean distance gives the shortest or minimum distance between two points, Manhattan has specific implementations.

For example, if we were to use a Chess dataset, the use of Manhattan distance is more appropriate than Euclidean distance. Another use would be when are interested in knowing the distance between houses which are few blocks apart.

Also, you might want to consider Manhattan distance if the input variables are not similar in type (such as age, gender, height, etc.). Due to the curse of dimensionality, we know that Euclidean distance becomes a poor choice as the number of dimensions increases.

So in a nutshell: Manhattan distance generally works only if the points are arranged in the form of a grid and the problem which we are working on gives more priority to the distance between the points only along with the grids, but not the geometric distance.


High-dimensional data

Most of the volume of a high-dimensional orange is in the skin, not the pulp. If a constant number of examples is distributed uniformly in a high-dimensional hypercube, beyond some dimensionality most examples are closer to a face of the hypercube than to their nearest neighbor.

And if we approximate a hypersphere by inscribing it in a hypercube, in high dimensions almost all the volume of the hypercube is outside the hypersphere. This is bad news for machine learning, where shapes of one type are often approximated by shapes of another.

In high dimensions, a curious phenomenon arises: the ratio between the nearest and farthest points approaches 1, i.e. the points essentially become uniformly distant from each other. This phenomenon can be observed for wide variety of distance metrics, but it is more pronounced for the Euclidean metric than, say, Manhattan distance metric.

The premise of nearest neighbor search is that “closer” points are more relevant than “farther” points, but if all points are essentially uniformly distant from each other, the distinction is meaningless.


Summary

유클리드 거리는 고차원에서는 도움이 되지 않는다. 차원이 커지면서 대부분 유사한 거리를 갖게 되기 때문이다. 하나의 점을 중심으로 원을 그리고, 그 위에 다른 점들이 있다고 생각하면 거리는 같다.

데이터의 차원이 다른 경우에도, shortest distance를 구하는 Euclidean distacne 보다는, 절대적인 L1 norm을 구하는 metric인 Manhattan distance가 낫다.

이런 점을 보완하려고 0~1 사이의 값을 갖도록 fraction을 쓰는 $L_f$ norm 같은 친구들도 있는듯.

직관적으로 생각해도 제곱을 해주는 유클리드 거리보다는 절댓값을 구하는 맨하튼이 해당 상황들에선 낫지 않을까?

The higher the norm index, the more it focuses on large values and neglects small ones. This is why the RMSE is more sensitive to outliers than the MAE.

norm의 지수가 클 수록 큰 값의 원소에 치우치고 작은 값은 무시되는 경향이 있다. high dimension에서 RMSE가 MAE보다 outlier에 취약한 이유도 같은 맥락.


관련 stackexchange 질문들

When would one use Manhattan distance as opposed to Euclidean distance?

Euclidean distance is usually not good for sparse data (and more general case)?

Why is Euclidean distance not a good metric in high dimensions?


GAN에서 distance를 사용하는 방법

GAN은 내 분야는 아니지만 어쩌다 읽은 논문에서 해당 주제를 다뤄서, 잠깐 정리해둔 것을 아래에 첨부한다. 조금 불친절하게 정리되어 있지만, 결국 GAN에서도 생성 모델 학습 과정에서 생성 모델이 만든 분포와 실제 타겟으로 하는 분포의 거리를 구한다는 것.


Generative Model

  • 학습 data의 분포를 학습해 해당 분포를 따르는 유사한 data를 생성하는 Model
  • P_g: 생성 모델이 만들어낸 분포
  • P_x: target으로 하는 분포
  • P_g -> P_x 로 만들 때 optimal transport는 발생한 평균 cost (P_g를 일부 변형시켜 P_g’를 만듦)의 하한


Optimal transport mapping

  • 두 공간을 어떻게 연결시켰을 때 가장 최적인 경로를 찾을 수 있을지


Wasserstein distance