Welcome to Machine Learning!
Andrew Ng 교수님의 Coursera 강좌 Machine Learning offered by Stanford Week 1 에 해당하는 내용입니다.
시작 전 여담이지만, 현재까지 이 강좌를 약 250만 명이 들었다고 했다. 그만큼 좋은 강의라는 걸 보여주는 지표이기도 하고, 머신러닝에 대한 관심이 얼마나 뜨거운지를 보여주기도 한다. 딱 2달 간 진행해서 12월까지 모두 수강하는 것이 목표이다 :) 열심히 들어서 Certificate 받아보자!
19/10/22 시작!
Introduction
Machine learning definition
- Arthur Samuel (1959): the field of study that gives computers the ability to learn without being explicitly programmed
- Tom Mitchell (1998): Well-posed Learning Problem: A computer program is said to learn from
experience Ewith respect to sometask Tand someperformance measure P, if its performance on T, as measured by P, improves with experience E.- Example: playing checkers.
- E = the experience of playing many games of checkers
- T = the task of playing checkers.
- P = the probability that the program will win the next game.
Machine Learning examples
- Handwriting recognition
- Natural Language Processing (NLP)
- Computer Vision
- Self-customizing programs (e.g., Amazon, Netflix)
- Understanding human learning (brain, real AI)
Machine Learning algorithms
- Supervised learning: task를 수행할 수 있는 방법을 컴퓨터에게 가르침
- Unsupervised learning: 컴퓨터가 스스로 학습하도록 유도
- Reinforcement Learning
- Recommender systems
Supervised learning
-
right answersgiven -
Regression: Predict continuous valued output -
Classification: Discrete valued output (0 or 1)- 분류에 쓰이는 속성이 1개일 수도 있고, 여러 개일 수도 있다.
Unsupervised learning
-
Clustering: 관련이 있는 것끼리 묶어주는 것 - e.g. social network analysis, market segmentation, astronomical data analysis
Cocktail party problem algorithm
Unsupervised learning이 적용된 예시로, 두 개의 음성 소스가 합쳐진 파일에서 각각의 음성 소스를 분리해내는 알고리즘이다. 놀랍게도 아래의 단 한 줄의 Octave 코드로 구현이 가능하다!
[W,s,v] = svd((repmat(sum(x,*x,1),size(x,1),1).*x)*x');
여기까지 전체적으로 다 아는 내용이여서, 간략하게 정리했다.
Linear Regression with One Variable
Cost Function
선형 회귀 모델과 cost function에 대해 간략하게 설명하셨다. 이는 이미 많이 다룬 내용이여서 설명을 생략하겠다. 특이점은 cost function 식을 다음과 같이 세우셨다는 것이다.
\[J(θ0,θ1)=\frac{1}{2m}\sum_{i=1}^{m}(\hat y_i−y_i)^2=\frac{1}{2m}\sum_{i=1}^{m}(h_θ(x_i)−y_i)^2\]맨 앞에 1/2가 들어가는데, 이는 식을 좀 더 쉬워 보이게 한다. 그리고 어떤 값의 반을 최소화하는 것은 θ0, θ1값을 최소화 하는 것과 같은 값의 과정을 가진다.
이 비용 함수 $J(θ0,θ1)$를 최소화해야 한다.
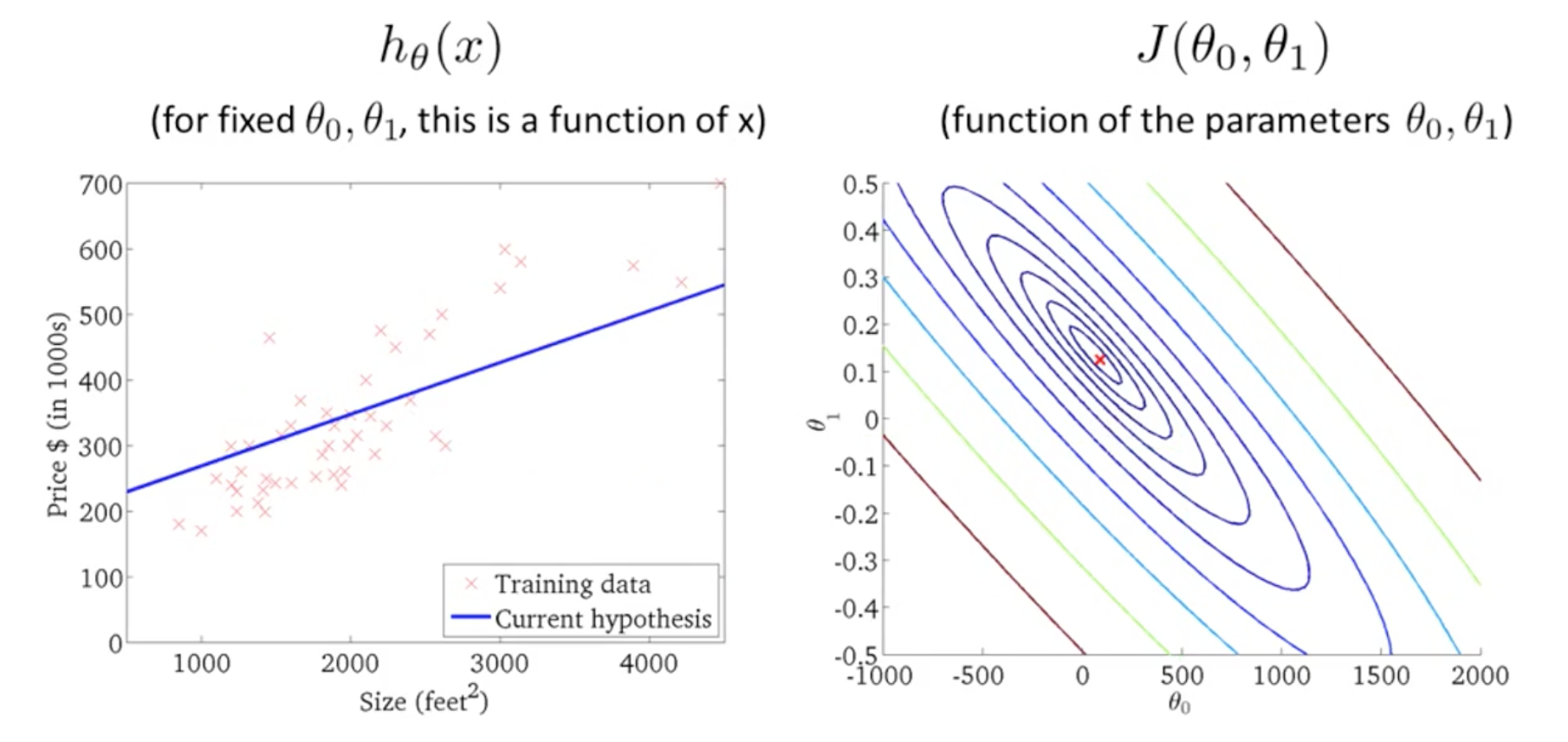
우리는 두 개의 parameter를 같는 비용함수 j를 등고선 그래프로 그려볼 수 있다. 비용함수 j의 최소값과 비슷할 수록 더 좋은 가설임을 알 수 있다.
Gradient Descent
The gradient descent algorithm is:
repeat until convergence:
\[θ_j:=θ_j−α\frac{∂}{∂θ_j}J(θ0,θ1)\]where
j=0,1 represents the feature index number.

이 알고리즘에서 주의할 것은 $θ0,θ1$를 동시에 바꾸어주고 update해줘야 한다는 것이다. 그렇지 않고 만약 오른쪽처럼 $θ0$를 먼저 update하면, $θ1$에는 바뀐 $θ0$가 적용되어 잘못된 값을 도출한다.
비용함수 j와 하나의 파라메터, $θ1$이 있다고 하자. 이 함수 j에서 미분계수 $\frac{d}{dθ_1}$는 곧 기울기 값, 함수의 탄젠트 값이다.
만약 이 미분계수 값이 양수이면, 식에 의해 $θ1$의 값 미분계수에 learning rate를 곱한만큼 작아진다. 즉, $θ1$가 감소한다.
반대로 이 미분계수 값이 음수이면, 식에 의해 $θ1$의 값 미분계수에 learning rate를 곱한만큼 커진다. 즉, $θ1$가 증가한다.
두 경우 모두, 그 전 값에서 최소값과 더 가까운 쪽으로 이동한다.
α는 learning rate로, 너무 작으면 너무 조금씩 이동해 하강 속도가 매우 느리다. 하지만 매우 크다면, 최소값보다 매우 가까운 경우에는 더 가버리거나 방향을 전환하는 것에 실패해 overshooting한다.
만약, $θ1$가 local minimum에 있는 경우에는 미분계수가 0이 된다. 그러면 $θ1$은 더이상 변화하지 않는다.
How does gradient descent converge with a fixed step size α?
Gradient descent can converge to a local minimum, even with the learning rate α fixed.
local minimum에 가까워질수록, 미분계수 값은 작아질 것이고, 같은 learning rate가 유지되기 때문에 하강 기울기는 더 조금씩 이동하게 된다. 그래서 우리는 α값을 감소시킬 필요가 없다.
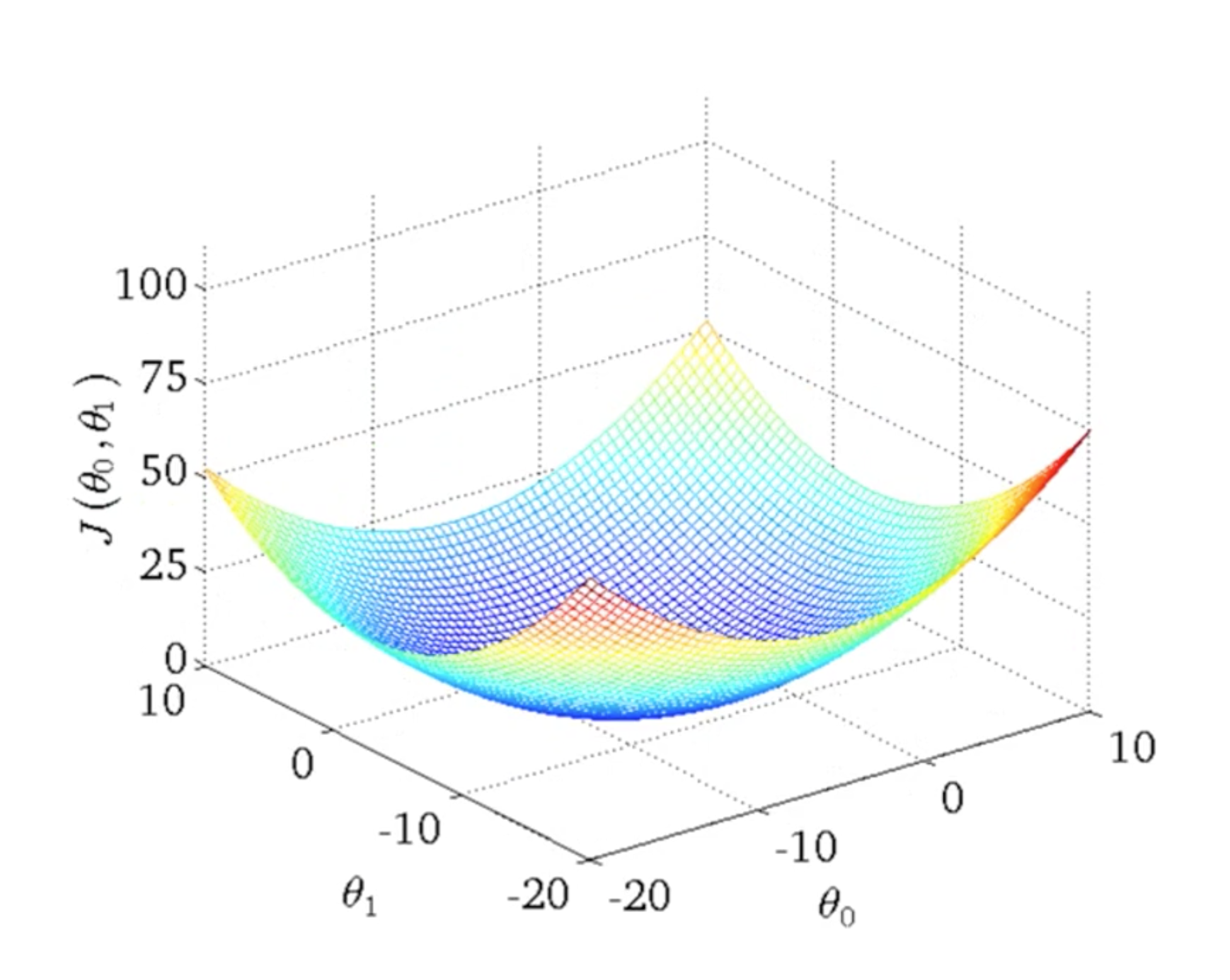
convex function은 볼록함수로, 다음과 같이 local minimum은 없고, global minimum만 있다. 보통 cost function의 parameter들은 처음에 0로 놓는다. 그리고 GDA를 적용해, global minimum을 찾을 때까지 반복한다.
이 알고리즘은 Batch Gradient Descent라고도 불린다.
자료의 범위나 크기가 너무 커서, GDA를 사용할 수 없을 때 반복최소이승법을 사용한다.
Linear Algebra Review
Matrices and Vectors

- Matrix: 2-dimensional arrays
- $A_{ij}$ refers to the element in the $i$th row and $j$th column of matrix A.
- 4x3행렬은 행이 4개, 열이 3개인 행렬이다.
- Vector: An $n\times1$ matrix
- $\Bbb R^n$는 n차원 벡터를 의미한다.
- $y_i$는 벡터의 i번째 원소를 의미한다.
- 실제 수학에서는 index가 1부터 시작하는 1-indexed가 일반적이지만, 머신러닝에서는 0부터 시작하는 0-indexed가 더 사용하기 편하다.
- 보통 행렬은 A,B,X,Y와 같이 대문자로 표기하고, 일반적인 벡터, 숫자, 자료값, 스칼라값은 a,b,x,y로 표기한다.
Addition and Scalar Multiplication
행렬의 덧셈, 행렬과 스칼라의 곱에 대한 설명은 제 기존 포스팅으로 대체합니다.
스칼라는 실수, real number를 의미한다. 그리고, 차원이 다른 두 행렬은 덧셈과 뺄셈이 불가능하다는 것에 유의하자.
Matrix Multiplication
Vector Multiplication
행렬과 벡터를 곱하면 어떻게 될까?
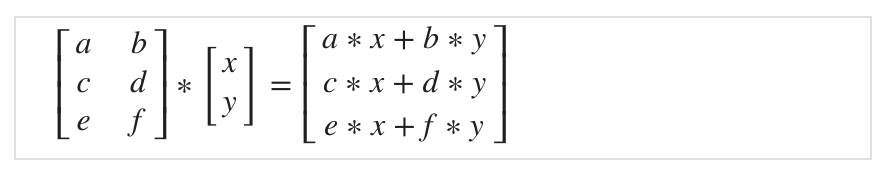
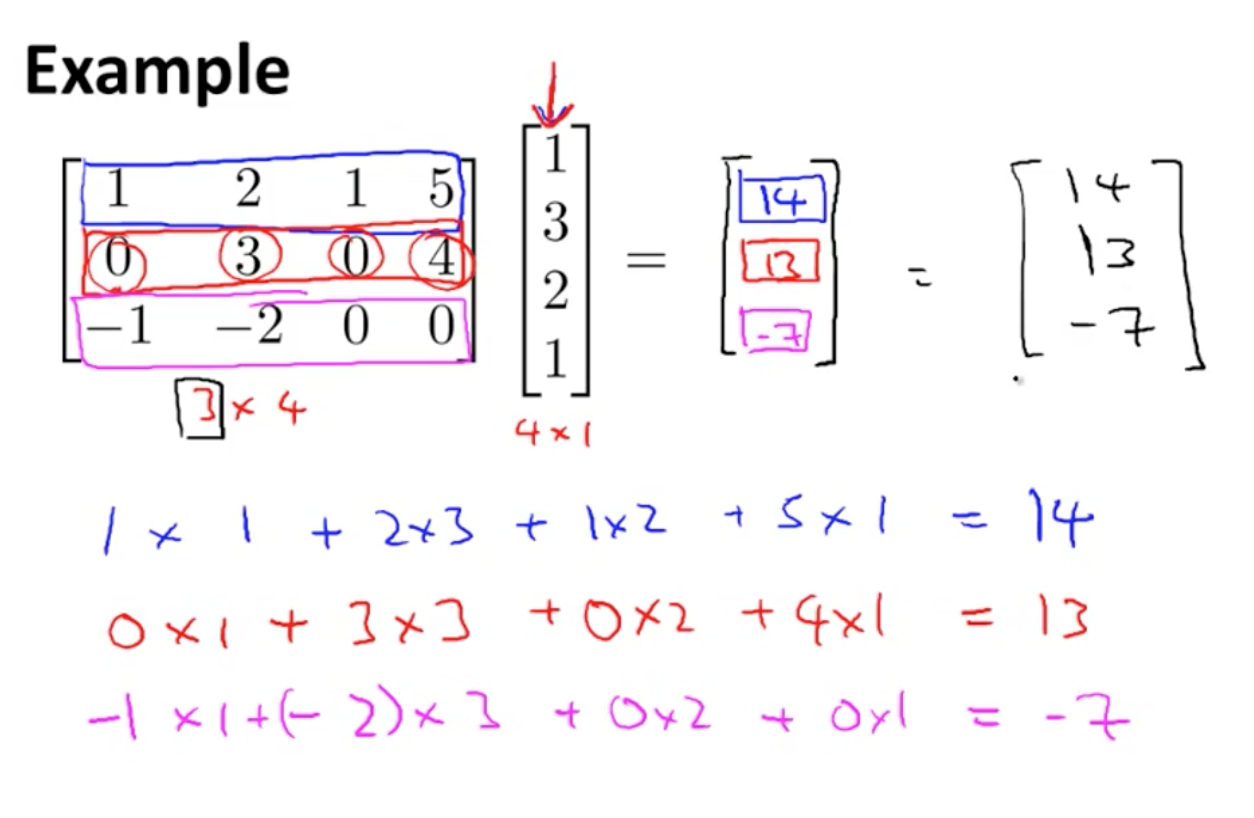
위와 같이 3x4 행렬과 4차원 벡터, 4x1 행렬을 곱하면 3차원 벡터, 3x1 행렬이 나오게 된다. 계산 과정은 그림을 참고하자. 결과값으로 행렬의 row x 벡터의 column (1)을 얻는다는 것을 기억하자.
우리는 이 곱셈법을 활용해 코딩에서 간단한 트릭을 쓸 수 있다.
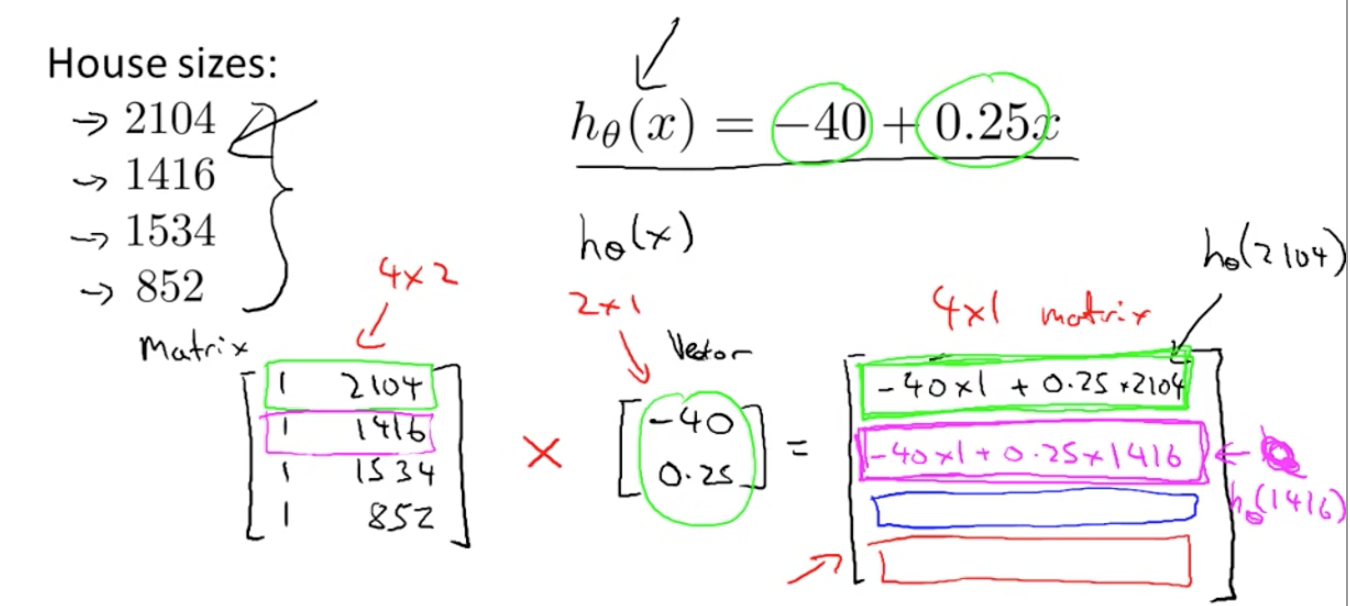
Prediction = Data Matrix x Parameters과 같이 vectorization, 코드로 벡터를 만들어서 더욱 효율적으로 모델의 결과값을 도출할 수 있다.
- 추가) 선형대수 수업을 듣고 나서
- 사실 이 트릭은 선형대수에서 연립일차방정식들을 행렬로 계산하는 수학적인 발상을 관통한다. 사실 변수는 가만히 있고, coefficient들만 바뀌기 때문에 계산을 쉽게 하기 위해 행렬을 도입했다. 이 regression에서 값을 도출하는 과정도 결국 coefficient들인 data만 변하기 때문에 행렬을 적용하면 훨씬 간단하게 계산이 가능한 것이다!
수학을 어디다 써먹냐던 문과가 수학을 공부하며 짜릿함을 느끼고 있는 순간이다.
Matrix Matrix Multiplication
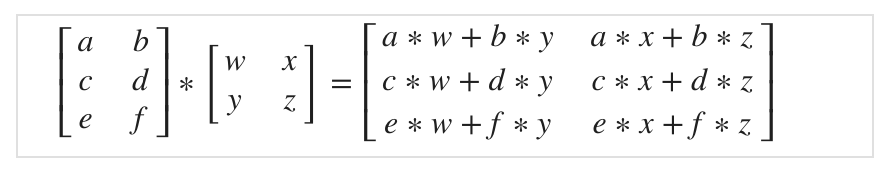
An m x n matrix multiplied by an n x o matrix results in an m x o matrix. In the above example, a 3x2 matrix times a 2x2 matrix resulted in a 3x2 matrix.
위에서 우리가 했던 행렬과 벡터의 곱셈을 곱하는 행렬의 column 개수 만큼 차례로 진행한다고 생각하면 쉽다.
Matrix Multiplication Properties
5x3과 3x5는 같다. 하지만, 행렬 곱에서는 행렬의 교환법칙이 성립하지 않는다.
$(A\times B)\times C = A\times (B\times C) $와 같이 결합법칙은 성립한다.
Identity matrix (항등 행렬)
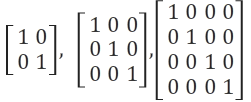
- 곱셈의 항등원이 1인 것처럼, 행렬 계산에서도 곱해도 변화를 주지 않는 항등 행렬이 존재한다.
- 항등행렬에서는 행렬 곱의 교환법칙이 성립한다.
- When multiplying the identity matrix before some other matrix (I∗A),
the square identity matrix's dimensionshould match the othermatrix's rows.
Inverse and Transpose
행렬에서는, m x m 형태인 square matrix, 정방행렬만이 역행렬을 갖는다. 행렬에 역행렬을 곱하면 항등 행렬이 나와야 하기 때문이다.
숫자 0이 역수가 없는 것처럼, 모든 원소가 0인 정방행렬도 역행렬이 없다. 이런식으로 역행렬이 없는 행렬이 몇 개 더 있다고 하셨는데, 따로 소개하시진 않았다.
0행렬과 같이 역행렬이 없는 행렬을 singular matrix 또는 degenerate matrix이라고 한다.
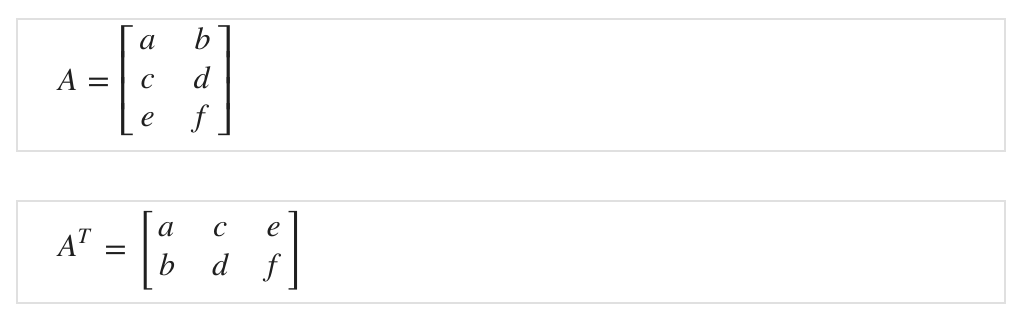
The transposition of a matrix is like rotating the matrix 90° in clockwise direction and then reversing it. Matrix Transpose, 전치행렬은 아래와 같이 행과 열을 바꾼 행렬이다.
이상으로 Week 1을 마무리했다.
19/10/27 끝!