Recommender systems 원서를 읽던 중에 두 식이 매우 유사해 차이를 정확하게 정리하려 한다.

우선 코사인 유사도, 피어슨 기반 유사도, adjusted 코사인 유사도의 식을 보겠다.

세 지표 모두 user-user간, 또는 item-item간 얼마나 유사한지를 나타내는 지표이다.

아래 식은 item-based collaborative filtering 과정에 대해 쓰여진 식입니다. user-based CF라면 그에 맞게 바꿔 생각해주시면 됩니다.

이미지 및 설명 출처


Cosine similarity

Also known as vector-based similarity, this formulation views two items and their ratings as vectors, and defines the similarity between them as the angle between these vectors:

두 벡터 간의 유사한 정도를 코사인 값으로 나타낸 것이다. -1부터 1까지의 값을 가지며, -1은 서로 전혀 다르고 1은 완전히 같은 경우를 의미한다.

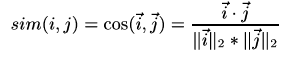
itembased-cosine


Pearson based similarity

This similarity measure is based on how much the ratings by common users for a pair of items deviate from average ratings for those items:

유저의 rating 기준은 유저마다 다를 수 있다. 1부터 5까지의 rating 범위를 갖는다고 하자. 어떤 positive 유저는 맘에 들지 않은 아이템에게도 3 이상의 값을 줄 수 있다. 반면 negative 유저는 조금이라도 취향에 맞지 않으면 1의 rating을 부여할 수도 있다. 따라서 이러한 different rating scales를 보정하기 위해 mean-centered rating을 사용한다.

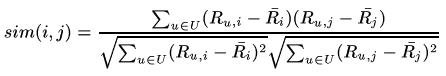
itembased-pearson

위 식과 같이 raw cosine에서 해당 item에 부여된 모든 rating의 평균값을 빼주어 보정한다.


Adjusted Cosine similarity

This similarity measurement is a modified form of vector-based similarity where we take into the fact that different users have different ratings schemes; in other words, some users might rate items highly in general, and others might give items lower ratings as a preference. To remove this drawback from vector-based similarity, we subtract average ratings for each user from each user’s rating for the pair of items in question:

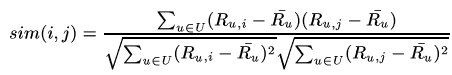
itembased-adjusted-cosine

mean-centered 보정을 해주는 것은 피어슨 상관계수 접근과 같지만, 빼주는 값이 mu_u로 같은 값이다. 피어슨 상관계수 식에서는 mu_i, mu_j로 각각 빼주는 값이 달랐는데 말이다. 이는 adjust cosine similarity를 구할 때는 item에 부여된 rating의 평균이 아니라, 해당 유저가 모든 아이템에 부여한 rating의 평균값을 빼주는 것이다.


Summary

두 유사도는 유사하지만, mean을 어떻게 구해주냐에 따라 전혀 다른 값을 가진다. 두 유사도가 같다는 오해를 하지 않길 바란다. 참고로, 원서에서는 item-based CF에서는 pearson-based보다 adjusted cosine이 더 성능이 높다고 했다. user-based에서는 pearson을 언급한 걸 보니 pearson이 더 효과적인 지표 아닐까..라고 추측한다. 언제 어떤 지표를 사용하는 것이 더 유리한지는 더 공부해보기.


User-based CF에서는?

Pearson based similarity
  • user-based에서는 item_i와 item_j간의 유사도가 아닌, user_i, user_j의 유사도를 구하기 때문에 유저 i, j 각각의 모든 rating의 평균을 빼주면 된다.
  • Strictly, 유저 i와 j가 공통적으로 rating을 남긴 item들에 대한 평균만 구해야한다. 하지만, 현실의 문제는 sparsity가 높기 때문에 그냥 전체 item의 평균을 사용한다고 한다.


Adjusted Cosine similarity
  • user_i, user_j가 공통적으로 rating을 남긴 item k의 rating 평균을 적용하면 되겠다.