베이즈 추정법과 최대가능도추정법
모수 추정의 끝판왕 친구들! 두 개념은 자주 쓰이지만, 처음 접하면 꽤 헷갈리는 개념이므로 확실하게 짚고 넘어가자! 인공지능을 위한 수학 책에서 내용의 일부를 발췌했다. (책 추천합니다. 하나 책꽂이에 있으면 든든해요.)
최대가능도추정
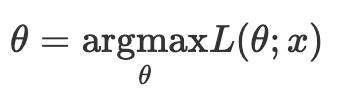
- Maximum Likelihood Estimation, MLE
- 최대가능도를 추정한다는 것은 파라미터 $\theta$에 대한 가능도함수 L($\theta$)를 최대화하는 모수 $\theta$ 값을 구하는 것이다.
- 이때, 최댓값을 가지는 지점은 1계 미분을 했을 때 $dL(\theta)/d\theta = 0$이 되는 지점이며, 이때의 $\theta$를 구하면 된다.
Example
예를 들어, 주사위를 던져 숫자 1이 나올 확률은 1/6이다.
하지만 단언할 수는 없기 때문에 확률을 미지의 수로 두고 실험을 해보자.
만약 100번을 던졌을 때, 숫자 1이 나온게 20번이라고 하자.
이때 1이 나올 확률을 $\theta$라고 두고, 위와 같은 결과가 나올 확률을 $L(\theta)$라고 하자. 그러면 아래와 같은 식이 나온다.
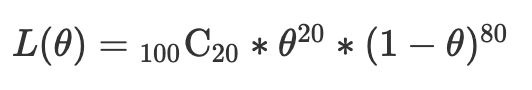
이 식을 구했으니, 이 식을 미분해 0이 나오는 $\theta$를 구하면 된다. 하지만, 이 식의 차수는 매우 높기 때문에 미분을 하기엔 복잡하다. 따라서, 이 가능도함수에 자연로그를 붙여주어 로그가능도함수를 만들어주면 편하다.
확률과 가능도의 차이
- 확률: 사건이 어떤 빈도로 일어날 것인지 나타낸 것
- 가능도: 관측된 값들을 생성할 가능성이 가장 높은 실제 모수를 추정. 이때의 가능성을 수치로 표현한 것이 가능도이다.
로그가능도함수
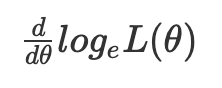
로그를 사용하면, 곱셈을 덧셈으로 바꿀 수 있어 고차 방정식을 1차 방정식 모양으로 바꿀 수 있다.
Summary
주사위 예제에서 로그가능도함수를 미분한 후 0이 되는 지점의 $\theta$를 찾으면, 0.2가 된다.
이를 통해 우리는 “어떤 주사위를 던졌을 때, 숫자 1이 나올 확률로 가장 그럴듯한 것은 0.2이다.”라는 결론을 얻을 수 있다.
파라미터가 여러 개인 경우는 각각의 파라미터에 대해 편미분을 하면 된다.
베이즈 추정법
최대가능도 추정법과 가장 다른 점은, 모수 $\theta$를 미지의 수로 보지 않고 확률변수로 본다는 점이다. 확률변수는 확률밀도함수를 갖고, 어떤 값이 가능성이 높고 어떤 값이 낮은지를 살펴본다는 것이다.
관찰을 통해 얻은 데이터는 사전분포에 따라 얻어진 결과이므로,
그에 대한 조건부확률을 구하면 된다.
라는 접근 방식으로 사후확률(조건부확률) 을 구한다. 결국 관측된 데이터를 기반으로 모수의 조건부 확률분포를 계산하는 작업이다.
베이즈 정리, 사후확률을 추정하는 식은 아래와 같다. B는 관측값, A는 실제값이라고 직관적으로 생각해보자.
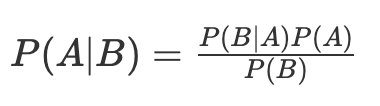
P(A|B): 사후확률
- 사건 B를 관측한 후에, 그 원인이 되는 사건 A의 확률을 따졌다는 의미
P(B|A): 우도
P(A): 사전확률
- 사전에 미래에 어떤 사건이 일어날 확률을 측정한 것
베이즈 추정법을 쓰는 이유
베이즈 추정법을 사용하는 이유는 추정된 모숫값 숫자 하나만으로는 추정의 신뢰도와 신뢰구간을 구할 수 없기 때문이다.
예를 들어 인터넷 쇼핑몰에 있는 두 개의 경쟁상품에 사용자 의견이 다음과 같이 붙어 있다고 하자.
상품 A: 전체 평가의견 3개, 좋아요 2개, 싫어요 1개
상품 B: 전체 평가의견 100개, 좋아요 60개, 싫어요 40개
내가 이 상품을 사용했을 때 평가의견이 ‘좋아요’가 나올지 ‘싫어요’가 나올지는 베르누이분포 확률변수로 모형화할 수 있다. 최대가능도 추정법에 따르면 상품 A와 상품 B에서 ‘좋아요’가 나온 비율을 사용하여 베르누이 모수를 구하면 다음과 같이 상품 A의 모수가 높다.
상품 A의 모수: $\frac{2}{3} = 0.67$ 상품 B의 모수: $\frac{60}{100} = 0.6$
상품 B의 평가의견은 100개고 상품 A의 평가의견은 3개밖에 되지 않는데 상품 A의 모수가 더 높다고 더 높은 상품이라고 확신할 수 있는가? 베이즈 추정법에서는 단순히 모수의 값을 하나의 숫자로 구하는 것이 아니므로 이러한 잘못된 결론을 내리지 않도록 도와준다.
베이즈 정리를 재밌게 정리한 블로그. 코난..🐶 기존 빈도론과 베이지안이 어떻게 다른지 설명한 블로그
Comparison
인공지능을 위한 수학 책에서는 둘을 다음과 같이 비교하고 있다. 둘 중 어느 것을 사용하더라도, 이는 모두 ‘추정’에 불과하므로 한계를 명확히 인지하고 데이터를 다뤄야 한다.
수학적으로 정확한 최대가능도추정법
- 진정한 확률 모델은 존재하며, 관찰된 데이터는 그러한 모델을 충실히 따르고 있다. 따라서, 시행을 반복하여 관찰하면 진정한 확률 모델이 보이기 시작할 것이다.
- 하지만, 실험을 무한하게 할 수는 없으니 우리는 가장 그럴듯한 확률, 관찰되는 데이터를 믿을 수 밖에 없다.
- 따라서 관찰 결과가 편향적이라면 치명적인 추정법이다. 시행 횟수가 충분해야 신뢰할 수 있다.
실용적이지만 의심스러운 베이즈추정법
- 지금까지의 관찰 결과를 근거로 사전분포를 가정한다. 이 사전분포에 따라 관찰 데이터가 얻어졌으므로, 그에 대한 조건부 확률을 구하면 된다고 한다.