아래 내용은 Khan Academy의 Linear Algebra 강의를 바탕으로 합니다.

Vectors

벡터와 스칼라

  • vector: magnitude + direction
  • 100km/h와 같은 speed(속력)은 방향이 없으므로, scalar
  • 동쪽으로 100km/h와 같은 velocity(속도)는 vector


벡터 표기법

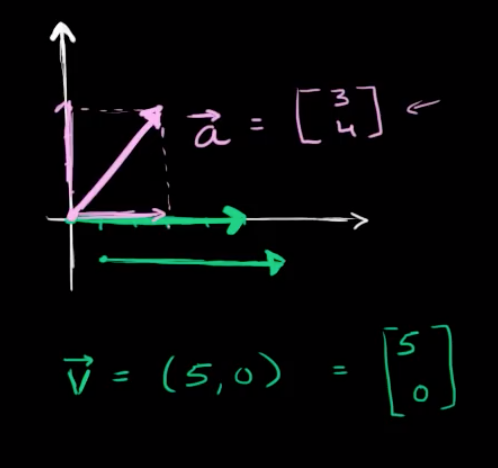
drawing_vector

벡터는 변수 위에 화살표를 그려서 벡터임을 나타낸다. 수식적 표기는 (수평 이동량, 수직 이동량)으로 나타내거나 다음과 같이 열 벡터로 나타낼 수도 있다.

\[\begin{bmatrix}n \\ m \end{bmatrix}\]

그림에서 초록색으로 표현된 벡터 두 개는 같은 벡터라고 할 수 있다. 어디에 표현하는지 중요하지 않고, 어느 방향으로, 얼마나 움직였는지가 중요하다. 그리고 보라색으로 표현된 벡터는 수평 방향으로 3, 수직 방향으로는 4 이동한 벡터이다. 피타고라스의 정리에 의해 벡터 크기는 5임을 구할 수 있다.

벡터는 시작점이 중요하지 않다. 시작점을 (x, y)라고 하자. 이 때 (-1, 2)의 벡터를 좌표 평면에 나타내려고 하면 (x-1, y-2)를 하면 된다. 만약 시작점이 (-4, 4)라면 이 점에서 (-5, 6)까지 벡터를 그리면 된다.


Real coordinate spaces

\[{\mathbb R^2}\]

이와 같은 표기는 2차원 실수좌표공간을 의미한다. R은 실수좌표공간을 의미하고, 2는 차원을 의미한다. 이는 결국 all possible real-valued 2-tuples 라고 할 수 있다.

  • 튜플 (Tuple): 순서가 정해진 숫자들의 리스트

위에서 언급한 all possible real-valued 2-tuples는 (3,4)와 같은 실수 2개의 숫자 리스트이다.

\[{\mathbb R^3}\]

이때는, 3차원 실수좌표공간을 의미한다. 예시로 3차원 벡터를 만들어보자.

\[\vec x = \begin{bmatrix}0 \\ 0 \\ 0 \end{bmatrix} \vec b = \begin{bmatrix}-1 \\ 5 \\ 3 \end{bmatrix}\]

벡터 x와 벡터 b는 모두 ${\mathbb R^3}$에 속하는 원소이다.

\[{\mathbb R^n}\]

차원이 아무리 높아지더라도, 우리는 그것을 n-tuple vector라고 수학적으로 표현할 수 있다.


벡터의 덧셈

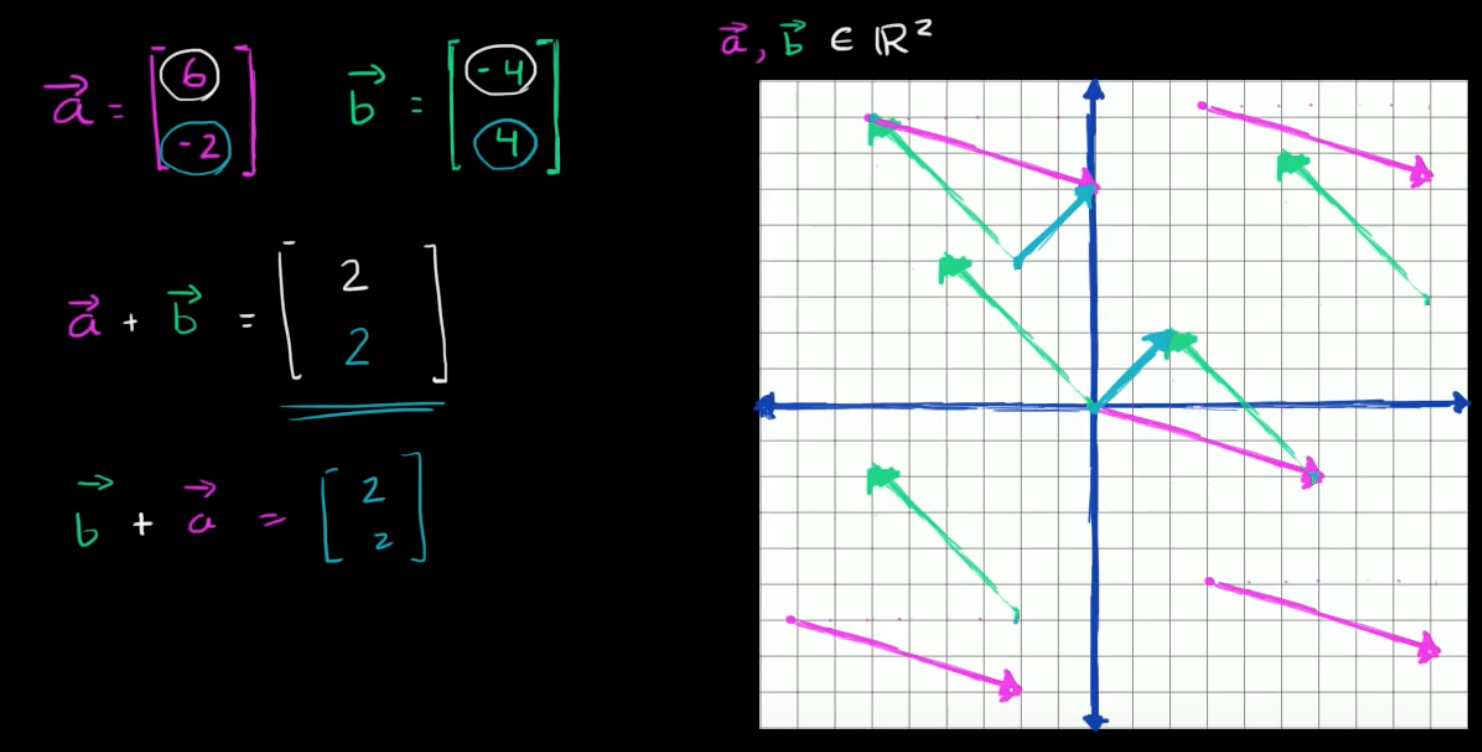
adding vectors

수식으로 나타내는 벡터의 합은 그냥 그림과 같이 성분끼리 더해주면 된다.

그래프로 나타내보면, 분홍색 벡터 a와 초록색 벡터 b를 더하면 파란색의 벡터를 얻을 수 있다. 원점에서 시작해 (6, -2)의 벡터 a를 그려보자. 그리고 도착점에서부터 (-4, 4)의 벡터 b를 더한다. 그리고 시작점에서부터 도착지점까지 벡터를 그리면 (2, 2) 벡터값을 구할 수 있다. 이는 수식으로 나타낸 벡터의 합과 같다.

벡터 b에 벡터 a를 더해도 값은 같다. 좌측 상단에 벡터 b를 그리고, 같은 방법으로 도착 지점에서부터 벡터 a를 그린다. 시작 지점에서 도착한 지점으로 벡터를 그리면 아까와 같이 (2, 2) 벡터값을 구할 수 있다.


벡터의 뺄셈

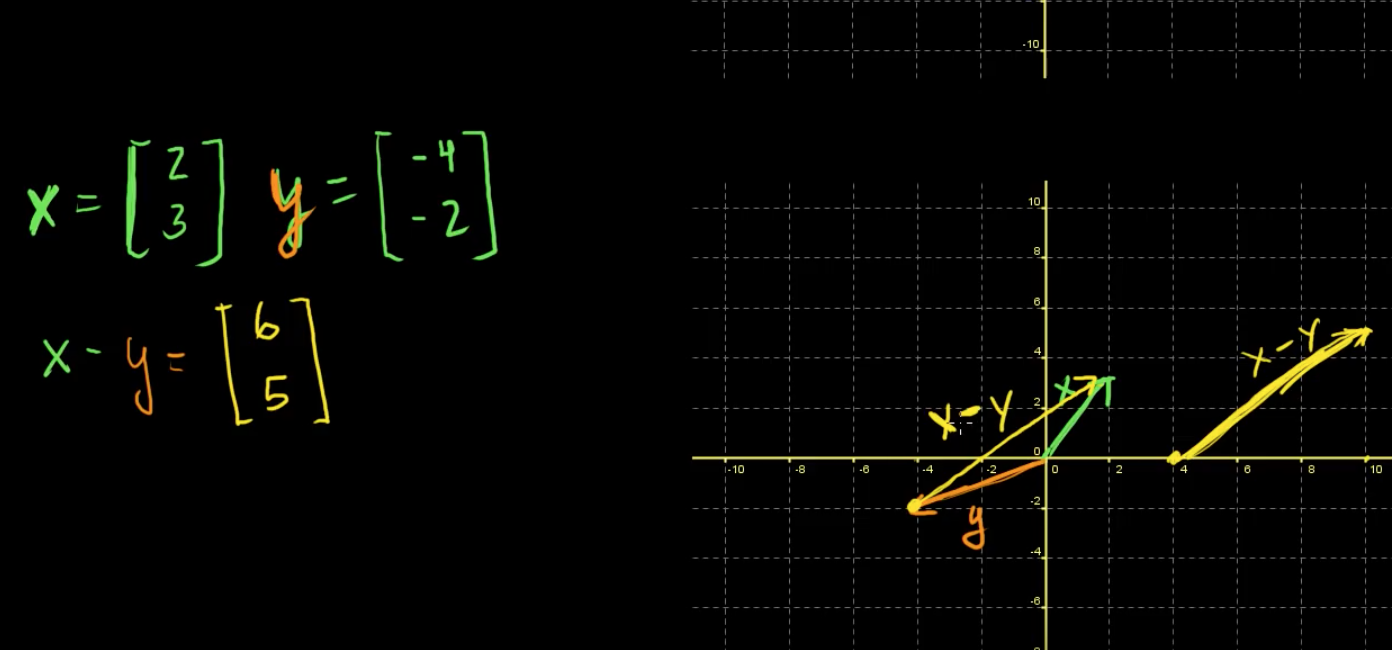
subtracting vectors

뺄셈도 덧셈과 같다. 벡터 x에서 벡터 y를 빼준다고 하면, x에 방향이 방향이 정반대인 벡터 y를 더해준다고 생각하면 쉽다.


벡터의 스칼라 곱셈

multiplying a vector (scalar)

수식으로 표현하는 곱셈 역시 어렵지 않다. 각각의 성분에 3을 곱한다. (2, 1)인 벡터 a에 3을 곱해 (6, 3)인 벡터를 얻을 수 있다. 초록색으로 그래프 상 나타내면 여전히 2차원 벡터이다. 방향은 바뀌지 않았지만, 크기는 바뀌었다. 벡터를 3배 확대했다고 생각하면 된다.

이번엔 벡터 a에 음수인 -1을 곱해보자. 이 때 벡터의 크기는 변하지 않았지만, 방향은 반대로 바뀌었다. 음수를 곱하면 방향이 바뀌게 된다.

이번엔 벡터 a에 -2를 곱해보자. 주황색으로 나타낸 이 벡터는 방향과 크기가 모두 바뀌었다.

💡 Tip: 벡터에 마이너스를 붙인 벡터는 방향만 정반대인 벡터이다.


단위 벡터 (Unit vectors)

단위 벡터는 방향만 가지고 있는, 크기가 1인 벡터이다. 단위벡터는 글자 위에 화살표 대신, \(\hat i\) hat을 넣는다.예시로, 아래와 같이 단위벡터 i와 j를 나타내볼 수 있다. 이는 표준 단위 벡터이기도 하다.

\(\hat i = (1,0)\), \(\hat j = (0,1)\)

모든 2차원 벡터를 $\hat i$와 $\hat j$의 합으로 구할 수 있다.

$\vec v = (2, 3)$일 때, $\vec v$는 $2\hat i+3\hat j$로 나타낼 수 있다. 또다른 벡터 b를 $\vec b = (-1, 4)$라고 했을 때, 벡터 v와 b의 합을 단위 벡터로 나타내면 \(\vec v+\vec b = \hat i+7\hat j\)이다. (1, 7)과 같은 표현이다.


단위 벡터 구하기

단위 벡터는 현재 벡터의 길이를 구한 후, 각 인자에 나누면 된다. 일반 벡터를 단위 벡터로 만드는 과정을 정규화라고도 한다.

예로, 벡터 v가 (3, 4)일 때, 단위 벡터를 구해보자. 벡터 (3, 4)의 길이는 $\sqrt{3^2\times4^2} = 5$이다. 단위벡터는 길이가 1이여야 하므로, 벡터 v의 성분들을 5로 나누어주면 길이가 1인 단위 벡터를 구할 수 있다. 따라서, 단위 벡터는 $(\frac35,\frac45)$이다.


매개변수 방정식

이 부분은 생소하고 어려워서 이해하는데 시간이 걸렸다.

자세한 그림과 설명은 이 곳을 참고하면 좋겠습니다.

$\vec v = (2,1)$일 때, 이 벡터 v와 동일 직선 상에 있는 벡터, collinear vector의 집합을 S라고 하자. 그러면 S는 다음과 같이 벡터와 스칼라의 곱으로 표현할 수 있다.

\[S = \{c\vec v \ | \ c \in \mathbb R\}\]

$2\vec v, 0.5\vec v, 10\vec v $ 모두 동일한 직선 위에 위치하는 벡터이다.

이 집합 S를 나타내는 선을 벡터 x의 크기만큼 이동한 집합을 L이라고 하면, 다음과 같이 집합 L을 표현할 수 있다.

\[L = \{\vec x + t\vec v \ | \ t \in \mathbb R\}\]

임의의 스칼라 $t$와 $\vec v$의 곱인 벡터에 $\vec x$를 더한다. 벡터의 종점들의 집합으로 직선 L을 정의할 수 있다. 이 벡터들\ $\mathbb R ^2$의 좌표상에 있는 점이라고 볼 수 있다. 선분을 수식이 아니라, 벡터의 집합으로도 표현할 수 있는 것이다.

기존에 우리가 방정식을 만들던 방법은 다음과 같다. 기울기 $m$과 어떤 한 점 $(0,b)$를 통해 $y=mx+b$와 같은 방정식을 만들었다.

이 때의 기울기 $m$이 두개의 벡터 $\vec a, \vec b$를 지나가는 선이라면 그 직선은 다음과 같이 나타낼 수 있다.

\[L = \{\vec b + t(\vec b-\vec a) \ | \ t \in \mathbb R\}\] \[L = \{\vec a + t(\vec b-\vec a) \ | \ t \in \mathbb R\}\]

$\vec a=(2,1), \vec b=(0,3)$이라고 하면, L은 다음과 같다.

\[L = \{\begin{bmatrix}0 \\ 3 \end{bmatrix} + t\begin{bmatrix}-2 \\ 2 \end{bmatrix}\ | \ t \in \mathbb R\}\]

위와 같은 집합 L을 이용하여 $x,y$의 좌표를 구할 수 있다.

\[x = 0 + (-2t)\] \[y = 3+2t\]

이렇게 나타내는 방법은 벡터가 3개 이상일 때, 즉 n차원일 때 유리하다. 3차원일 때를 예로 보자.

parametric-rep-three-d

각 축을 $x, y, z$라고 했을 때 $x+y+z=k$이다. 이 때, $k$는 선이 아니라 plane이다. 각각의 좌표는 다음과 같이 구할 수 있다.

\[x=-1-1t\] \[y=2-1t\] \[z=7+3t\]

위 식들은 3차원 공간에서의 직선의 방정식이다. 이는 전에 없던 문제를 선형대수학에서 다루는 것을 보여준다.